题目内容
【题目】如图所示,参加某电视台娱乐节目的选手从较高的平台上以水平速度跃出后,落在水平传送带上。已知平台与传送带的高度差H=1.8m,水池宽度s0=1.2m,传送带AB间的距离L0=20m。由于传送带足够粗糙,假设选手落到传送带上后瞬间相对传送带静止,经过△t=1.0s反应时间后,立刻以a=2m/s2恒定向右的加速度跑至传送带最右端。
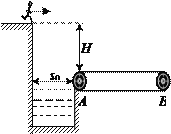
(1)若传送带静止,选手以v0=3m/s的水平速度从平台跃出,求这位选手落在传送带上距离A点的距离。(2)求刚才那位选手从开始跃出到跑至传送带右端所经历的时间。
(3)若传送带以v=1m/s的恒定速度向左运动,选手要能到达传送带右端,则他从高台上跃出的水平速度v1至少为多大?(g=10m/s2,计算结果均保留2位有效数字)
【答案】(1) Δs=0.6m;(2)t=6.0 s;(3) 4.1 m/s
【解析】
试题(1)从开始跃出到跑至传送带右端经历的时间经历两个过程:平抛运动和匀加速直线运动.因为平抛运动在竖直方向上做自由落体运动,在水平方向上做匀速直线运动,求出水平位移,然后再求出匀加速运动的位移以及时间.(2)选手平抛运动到传送带上后,在反应时间内跟传送带一起向左做匀速,然后以2m/s2的加速度向左做匀减速直线运动到0,如果在这段时间内未掉入水中,则不会落入水中,以后向右做初速度为0的匀加速直线运动.(1)选手离开平台后做平抛运动,在竖直方向上有:
![]()
得t1=![]()
在水平方向上有:s1=v0t1=1.8m
选手在传送带上做匀加速运动的位移s2=L0-(s1-s0)=![]()
得t2=4.4s
则选手运动的总时间t=t1+t2+△t=6.0s
(2)设水平跃出的速度为v1,落到传送带上1.0 s反应时间内向左发生的位移大小为:
s3=v△t=1m
然后向左减速至速度为零又向左发生位移s4=![]() =0.25m
=0.25m
不从传送带上掉下,平抛水平位移s≥s0+s3+s4=2.45m
则v1≥![]() =4.08m/s
=4.08m/s
所以选手从高台上跃出的水平速度最小为4.08m/s.