题目内容
19. 如图所示,用细绳一端系着质量为0.2kg的物体A静止在水平转盘上,细绳另一端通过转盘中心的光滑小孔O吊着质量为0.3kg的小球B,A的重心到O点的距离为0.2m,若A与转盘间的最大静摩擦力为2N,为使小球B保持静止,求转盘绕中心O旋转的角速度ω的取值范围.(g=10m/s2)
如图所示,用细绳一端系着质量为0.2kg的物体A静止在水平转盘上,细绳另一端通过转盘中心的光滑小孔O吊着质量为0.3kg的小球B,A的重心到O点的距离为0.2m,若A与转盘间的最大静摩擦力为2N,为使小球B保持静止,求转盘绕中心O旋转的角速度ω的取值范围.(g=10m/s2)
分析 当角速度取最小值时,A所受的静摩擦力背离圆心,当角速度为最大值时,A所受的静摩擦力指向圆心,结合牛顿第二定律求出角速度的范围.
解答 解:当角速度为所求范围的最小值ω1时,由牛顿第二定律有:
$T-f={m}_{A}r{{ω}_{1}}^{2}$,
且T=mBg,
由以上两式代入数据解得ω1=5rad/s.
当角速度为所求范围的最大值ω2时,由牛顿第二定律有:
$T+f={m}_{A}r{{ω}_{2}}^{2}$,
T=mBg,
由以上两式代入数据解得${ω}_{2}=5\sqrt{5}rad/s$.
则ω的范围为$5rad/s≤ω≤5\sqrt{5}rad/s$.
答:转盘绕中心O旋转的角速度ω的取值范围为$5rad/s≤ω≤5\sqrt{5}rad/s$.
点评 解决本题的关键知道圆周运动向心力的来源,抓住绳子的拉力不变,结合两个临界状态,运用牛顿第二定律进行求解.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
10.关于电容器的电容,下列说法正确的是( )
| A. | 电容器的电容只由它本身的特性决定 | |
| B. | 电容器两板电压越低,电容越大 | |
| C. | 电容器不带电时,其电容为零 | |
| D. | 电容器所带电荷量越多,电容越大 |
4.下列说法正确的是( )
| A. | 产生多普勒效应的原因是波源频率发生了变化 | |
| B. | 光的偏振现象说明光是一种纵波 | |
| C. | 全息照相利用了光的干涉原理 | |
| D. | 医学上用激光做“光刀”来进行手术,主要是利用了激光相干性好的特点 |
11.氢原子能级如图所示,一群原处于n=4能级的氢原子跃迁到n=1能级的过程中( )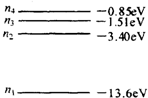
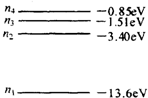
| A. | 能释放六种频率不同的光子 | |
| B. | 由n=2能级跃迁到n=1能级释放的光子频率最小 | |
| C. | 释放的光子的最大能量为12.75eV,最小能量为0.66eV | |
| D. | 由n=4能级跃迁到n=1能级释放的光子波长最长 |
8.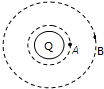 如图所示,A,B两带电小球都绕固定的电荷Q作匀速圆周运动,(A,B间库伦力不计,向心力就是Q的引力),B的轨道半径大于A的轨道半径,则( )
如图所示,A,B两带电小球都绕固定的电荷Q作匀速圆周运动,(A,B间库伦力不计,向心力就是Q的引力),B的轨道半径大于A的轨道半径,则( )
 如图所示,A,B两带电小球都绕固定的电荷Q作匀速圆周运动,(A,B间库伦力不计,向心力就是Q的引力),B的轨道半径大于A的轨道半径,则( )
如图所示,A,B两带电小球都绕固定的电荷Q作匀速圆周运动,(A,B间库伦力不计,向心力就是Q的引力),B的轨道半径大于A的轨道半径,则( )| A. | 如果A,B带电量相等,A的电势能小于B的电势能 | |
| B. | 如果A,B荷质比相同,A的速率大于B的速率 | |
| C. | 如果A,B荷质比相同,A的加速度小于B的加速度 | |
| D. | 不管A,B荷质比是否相同,A的速度一定大于B的速度 |
9.关于玻尔原子理论的基本假设,下列说法中正确的是( )
| A. | 原子中的电子绕原子核做圆周运动,库仑力提供向心力 | |
| B. | 电子绕核运动的轨道半径只能取某些特定的值,而不是任意的 | |
| C. | 原子的能量包括电子的动能和势能,电子动能可取任意值,势能只能取某些分立值 | |
| D. | 电子由一条轨道跃迁到另一条轨道上时,辐射(或吸收)的光子频率等于电子绕核运动的频率 |

 如图所示,水平放置的弹簧左端固定,小物块P(可视为质点)置于水平桌面上的A点,并与弹簧右端接触,此时弹簧处于原长.现用水平向左的推力将P缓慢地推至B点,此时弹簧的弹性势能为EP=21J.撤去推力后,P沿桌面滑上一个停在光滑水平地面上的长木板Q上,已知P、Q的质量分别为m=2kg、M=4kg,A、B间的距离Ll=4m,A距桌子边缘C的距离L2=2m,P与桌面及P与Q间的动摩擦因数都为μ=0.1,g取10m/s2,求:
如图所示,水平放置的弹簧左端固定,小物块P(可视为质点)置于水平桌面上的A点,并与弹簧右端接触,此时弹簧处于原长.现用水平向左的推力将P缓慢地推至B点,此时弹簧的弹性势能为EP=21J.撤去推力后,P沿桌面滑上一个停在光滑水平地面上的长木板Q上,已知P、Q的质量分别为m=2kg、M=4kg,A、B间的距离Ll=4m,A距桌子边缘C的距离L2=2m,P与桌面及P与Q间的动摩擦因数都为μ=0.1,g取10m/s2,求: