题目内容
9.2013年12月2日,我国成功发射了“嫦娥三号”探月卫星.“嫦娥三号”着陆前子啊距月球表面100km高度的轨道上做圆周运动,这比“嫦娥二号”距月球表面200km的圆形轨道更有利于对月球表面做出精细测绘.已知月球的质量为地球质量的$\frac{1}{81}$,月球的半径约为地球半径的$\frac{1}{4}$,地球半径为6.4×106m,地球表面附近的重力加速度为9.8m/s2.估算:(结果可保留根式)(1)月球表面重力加速度的值
(2)“嫦娥二号”与“嫦娥三号”在各自圆轨道上运行速度的比值.
分析 (1)星球表面重力与万有引力相等,求得重力加速度的表达式,再根据地月半径质量关系和地球表面的重力加速度求得月球表面的重力加速度;
(2)根据万有引力提供圆周运动向心力,由轨道半径关系求得线速度之比.
解答 解:(1)物体在星球表面受到的重力等于万有引力,
即:G$\frac{Mm}{{R}^{2}}$=mg,解得:g=$\frac{GM}{{R}^{2}}$,
$\frac{{g}_{月}}{{g}_{地}}$=$\frac{\frac{G{M}_{月}}{{R}_{地}^{2}}}{\frac{G{M}_{地}}{{R}_{地}^{2}}}$=$\frac{{M}_{月}{R}_{地}^{2}}{{{M}_{地}R}_{月}^{2}}$,
解得:g月=1.9 m/s2;
(2)设探月卫星圆轨道半径为r,
由牛顿第二定律得:G$\frac{Mm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$,解得:v=$\sqrt{\frac{GM}{r}}$,
对于“嫦娥二号”r1=R月+200 km=1800 km
对于“嫦娥三号”r2=R月+100 km=1700 km
“嫦娥二号”与“嫦娥三号”在各自圆轨道上运行速度的大小之比为:
$\frac{{v}_{1}}{{v}_{2}}$=$\sqrt{\frac{{r}_{2}}{{r}_{1}}}$=$\sqrt{\frac{17}{18}}$≈0.97.
答:(1)月球表面附近的重力加速度是1.9 m/s2;
(2)“嫦娥一号”与“嫦娥二号”在各自圆轨道上运行速度的大小之比为0.97.
点评 求一个物理量之比,我们应该把这个物理量先用已知的物理量表示出来,再根据表达式进行比较.
向心力的公式选取要根据题目提供的已知物理量或所求解的物理量选取应用.

 如图所示,在光滑的水平面上有一小球a以初速度v0运动,同时刻在它正上方有一小球b也以初速度v0水平抛出,并落于c点,则( )
如图所示,在光滑的水平面上有一小球a以初速度v0运动,同时刻在它正上方有一小球b也以初速度v0水平抛出,并落于c点,则( )| A. | 小球a先到达c点 | B. | 小球b先到达c点 | C. | 两球同时到达c点 | D. | 不能确定 |

| A. | 0-t1时间小球加速度减小 | |
| B. | t1-t2时间小球、弹簧和地球组成的系统机械能减少 | |
| C. | t1-t3时间小球动能先增大后减小 | |
| D. | t3-t4时间弹簧弹性势能变化量大小大于小球动能变化量大小 |
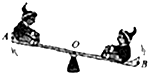 如图所示,翘翘板的支点O位于板上某一位置,A、B是板的两个端点,OA>OB.在翘翘板转动的某一时间,A、B的线速度大小分别为VA、VB,角速度大小分别为ωA、ωB,则( )
如图所示,翘翘板的支点O位于板上某一位置,A、B是板的两个端点,OA>OB.在翘翘板转动的某一时间,A、B的线速度大小分别为VA、VB,角速度大小分别为ωA、ωB,则( )| A. | vA>vB,ωA=ωB | B. | vA<vB,ωA=ωB | C. | vA=vB,ωA>ωB | D. | vA=vB,ωA<ωB |
 如图所示小球固定在轻杆的一端,轻杆绕O点转动,小球在竖直面内做完整的圆周运动,圆周运动的半径为L.则( )
如图所示小球固定在轻杆的一端,轻杆绕O点转动,小球在竖直面内做完整的圆周运动,圆周运动的半径为L.则( )| A. | 小球在最高点的速度V≥$\sqrt{gL}$ | |
| B. | 小球在最低点的速度V′≥$\sqrt{5gL}$ | |
| C. | 小球在最高点时,轻杆对小球的作用力方向一定向下 | |
| D. | 小球在最低点时,轻杆对小球的作用力方向一定向上 |
 如图(a),直线MN表示某电场中一条电场线,a、b是线上的两点,将一带负电荷的粒子从a点处由静止释放,粒子从a运动到b过程中的v-t图线如图(b)所示,设a、b两点的电势分别为φa、φb,场强大小分别为Ea、Eb,粒子在a、b两点的电势能分别为EPa、EPb,不计重力,则有( )
如图(a),直线MN表示某电场中一条电场线,a、b是线上的两点,将一带负电荷的粒子从a点处由静止释放,粒子从a运动到b过程中的v-t图线如图(b)所示,设a、b两点的电势分别为φa、φb,场强大小分别为Ea、Eb,粒子在a、b两点的电势能分别为EPa、EPb,不计重力,则有( )| A. | φa<φb | B. | Ea=Eb | C. | Ea<Eb | D. | EPa>EPb |
| A. | 全息照相利用了激光方向性好的特点 | |
| B. | 光速不变原理指出光在真空中传播速度的大小在不同惯性参考系中都是相同的 | |
| C. | 变化的电场一定产生变化的磁场,变化的磁场一定产生变化的电场 | |
| D. | 声源与观察者相对靠近时,观察者所接收的频率小于声源振动的频率 |
 某同学用图示装置描绘平抛物体的轨迹,实验简要步骤如下:
某同学用图示装置描绘平抛物体的轨迹,实验简要步骤如下: 如图所示,用细绳一端系着质量为0.2kg的物体A静止在水平转盘上,细绳另一端通过转盘中心的光滑小孔O吊着质量为0.3kg的小球B,A的重心到O点的距离为0.2m,若A与转盘间的最大静摩擦力为2N,为使小球B保持静止,求转盘绕中心O旋转的角速度ω的取值范围.(g=10m/s2)
如图所示,用细绳一端系着质量为0.2kg的物体A静止在水平转盘上,细绳另一端通过转盘中心的光滑小孔O吊着质量为0.3kg的小球B,A的重心到O点的距离为0.2m,若A与转盘间的最大静摩擦力为2N,为使小球B保持静止,求转盘绕中心O旋转的角速度ω的取值范围.(g=10m/s2)