题目内容
7.物理小组在一次探究活动中测量滑块在斜面上的加速度.实验装置如图1所示,打点计时器固定在斜面上.滑块拖着穿过打点计时器的纸带从斜面上滑下,如图2所示.图3是打出纸带的一段.
①已知打点计时器使用的交流电频率为f,选A、B、C…等7个点为计数点,各计数点间均有一个点没有画出,分别测出相邻两个计数点之间的距离,如图2所示,计算打下D点的速度大小表达式是 VD=$\frac{{S}_{3}+{S}_{4}}{4}f$.计算滑块下滑的加速度的表达式是:a=$\frac{({S}_{4}+{S}_{5}+{S}_{6})-({S}_{1}+{S}_{2}+{S}_{3})}{36}{f}^{2}$.
②该实验还可以测量滑块所受的摩擦力,下列物理量中还应测量的有ABD.(填入所选物理量前的字母,已知重力加速度为g)
A.木板的长度L B.木板的末端被垫起的高度h
C.木板的质量m1 D.滑块的质量m2
E.滑块运动的时间t
③测量②中所选定的物理量需要的实验器材是刻度尺、天平.
分析 由△s=aT2可求加速度,对物体受力分析,求合力由牛顿第二定律得摩擦力,由f=μN得μ,夹角由斜面的高、长求出;最后根据实验原理,从而确定实验器材.
解答 解:(1)根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,有:
vD=$\frac{{x}_{CE}}{{t}_{CE}}$=$\frac{{S}_{3}+{S}_{4}}{4}f$
由△s=aT2得:
a=$\frac{({S}_{4}+{S}_{5}+{S}_{6})-({S}_{1}+{S}_{2}+{S}_{3})}{(6T)^{2}}$=$\frac{({S}_{4}+{S}_{5}+{S}_{6})-({S}_{1}+{S}_{2}+{S}_{3})}{36}{f}^{2}$
(2)对物体受力分析求合力时,用到斜面的倾角,可由斜面的高、长表示斜面倾角正弦,故还应测量的有木板的长度L和木板的末端被垫起的高度h,同时加之滑块的质量m2;
故选:ABD.
(3)测量(2)中所选定的物理量需要刻度尺测量长度,用天平测量滑块的质量m2.
故答案为:①$\frac{{S}_{3}+{S}_{4}}{4}f$,$\frac{({S}_{4}+{S}_{5}+{S}_{6})-({S}_{1}+{S}_{2}+{S}_{3})}{36}{f}^{2}$;
②ABD;③刻度尺、天平.
点评 本题要能够通过纸带求解加速度,难点是根据牛顿第二定律求解出动摩擦因素的表达式进行分析.

练习册系列答案
相关题目
17.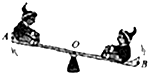 如图所示,翘翘板的支点O位于板上某一位置,A、B是板的两个端点,OA>OB.在翘翘板转动的某一时间,A、B的线速度大小分别为VA、VB,角速度大小分别为ωA、ωB,则( )
如图所示,翘翘板的支点O位于板上某一位置,A、B是板的两个端点,OA>OB.在翘翘板转动的某一时间,A、B的线速度大小分别为VA、VB,角速度大小分别为ωA、ωB,则( )
 如图所示,翘翘板的支点O位于板上某一位置,A、B是板的两个端点,OA>OB.在翘翘板转动的某一时间,A、B的线速度大小分别为VA、VB,角速度大小分别为ωA、ωB,则( )
如图所示,翘翘板的支点O位于板上某一位置,A、B是板的两个端点,OA>OB.在翘翘板转动的某一时间,A、B的线速度大小分别为VA、VB,角速度大小分别为ωA、ωB,则( )| A. | vA>vB,ωA=ωB | B. | vA<vB,ωA=ωB | C. | vA=vB,ωA>ωB | D. | vA=vB,ωA<ωB |
18.下列说法中正确的是( )
| A. | 全息照相利用了激光方向性好的特点 | |
| B. | 光速不变原理指出光在真空中传播速度的大小在不同惯性参考系中都是相同的 | |
| C. | 变化的电场一定产生变化的磁场,变化的磁场一定产生变化的电场 | |
| D. | 声源与观察者相对靠近时,观察者所接收的频率小于声源振动的频率 |
2. 如图所示,A、B两小球用细线跨过半径为R的光滑圆柱,圆柱固定在地面上.已知mB>mA,且$\frac{m_B}{m_A}$=k,一开始两球与圆柱轴心等高,在B球释放后直到A球沿圆柱面上升到最高点的过程中(A到达最高点时,B未落地)( )
如图所示,A、B两小球用细线跨过半径为R的光滑圆柱,圆柱固定在地面上.已知mB>mA,且$\frac{m_B}{m_A}$=k,一开始两球与圆柱轴心等高,在B球释放后直到A球沿圆柱面上升到最高点的过程中(A到达最高点时,B未落地)( )
 如图所示,A、B两小球用细线跨过半径为R的光滑圆柱,圆柱固定在地面上.已知mB>mA,且$\frac{m_B}{m_A}$=k,一开始两球与圆柱轴心等高,在B球释放后直到A球沿圆柱面上升到最高点的过程中(A到达最高点时,B未落地)( )
如图所示,A、B两小球用细线跨过半径为R的光滑圆柱,圆柱固定在地面上.已知mB>mA,且$\frac{m_B}{m_A}$=k,一开始两球与圆柱轴心等高,在B球释放后直到A球沿圆柱面上升到最高点的过程中(A到达最高点时,B未落地)( )| A. | 系统重力势能的减少是(mA-mB)gR | |
| B. | 系统重力势能的减少是($\frac{π}{2}$mB-mA)gR | |
| C. | 系统动能的增加是(mA+mB)gR | |
| D. | A球到达圆柱体最高点时的速度大小为$\sqrt{\frac{{gR({kπ-2})}}{k+1}}$ |
12.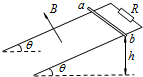 如图所示,一对足够长的光滑平行金属轨道,其轨道平面与水平面成θ角,上端用一电阻R相连,处于方向垂直轨道平面向上的匀强磁场中.质量为m、电阻为r的金属杆ab,从高为h处由静止释放,下滑一段时间后,金属杆开始以速度v匀速运动直到轨道的底端.金属杆始终保持与导轨垂直且接触良好,轨道电阻及空气阻力均可忽略不计,重力加速度为g.则( )
如图所示,一对足够长的光滑平行金属轨道,其轨道平面与水平面成θ角,上端用一电阻R相连,处于方向垂直轨道平面向上的匀强磁场中.质量为m、电阻为r的金属杆ab,从高为h处由静止释放,下滑一段时间后,金属杆开始以速度v匀速运动直到轨道的底端.金属杆始终保持与导轨垂直且接触良好,轨道电阻及空气阻力均可忽略不计,重力加速度为g.则( )
 如图所示,一对足够长的光滑平行金属轨道,其轨道平面与水平面成θ角,上端用一电阻R相连,处于方向垂直轨道平面向上的匀强磁场中.质量为m、电阻为r的金属杆ab,从高为h处由静止释放,下滑一段时间后,金属杆开始以速度v匀速运动直到轨道的底端.金属杆始终保持与导轨垂直且接触良好,轨道电阻及空气阻力均可忽略不计,重力加速度为g.则( )
如图所示,一对足够长的光滑平行金属轨道,其轨道平面与水平面成θ角,上端用一电阻R相连,处于方向垂直轨道平面向上的匀强磁场中.质量为m、电阻为r的金属杆ab,从高为h处由静止释放,下滑一段时间后,金属杆开始以速度v匀速运动直到轨道的底端.金属杆始终保持与导轨垂直且接触良好,轨道电阻及空气阻力均可忽略不计,重力加速度为g.则( )| A. | 金属杆加速运动过程中的平均速度小于$\frac{v}{2}$ | |
| B. | 金属杆加速运动过程中重力做功的功率大于克服安培力做功的功率 | |
| C. | 当金属杆的速度为$\frac{v}{4}$时的加速度大小是速度为$\frac{v}{2}$时加速度大小的2倍 | |
| D. | 整个运动过程中金属杆损失的机械能等于电阻R产生的焦耳热 |
17.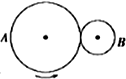 如图所示,A、B是两个依靠摩擦传动轮,两轮半径大小关系为RA=2RB,则两轮边缘上的( )
如图所示,A、B是两个依靠摩擦传动轮,两轮半径大小关系为RA=2RB,则两轮边缘上的( )
 如图所示,A、B是两个依靠摩擦传动轮,两轮半径大小关系为RA=2RB,则两轮边缘上的( )
如图所示,A、B是两个依靠摩擦传动轮,两轮半径大小关系为RA=2RB,则两轮边缘上的( )| A. | 转速之比nA:nB=1:2 | B. | 周期之比TA:TB=1:2 | ||
| C. | 向心加速度之比aA:aB=2:1 | D. | 角速度之比ωA:ωB=1:1 |
 如图所示,ABC为一固定的半圆形轨道,轨道半径R=0.4m,A、C 两点在同一水平面上,B点为轨道最低点.现从A点正上方h=2m的地方以v0=4m/s的初速度竖直向下抛出一质量m=2kg的小球(可视为质点),小球刚好从A点切入半圆轨道.不计空气阻力,取g=10m/s2.
如图所示,ABC为一固定的半圆形轨道,轨道半径R=0.4m,A、C 两点在同一水平面上,B点为轨道最低点.现从A点正上方h=2m的地方以v0=4m/s的初速度竖直向下抛出一质量m=2kg的小球(可视为质点),小球刚好从A点切入半圆轨道.不计空气阻力,取g=10m/s2. 如图所示,用细绳一端系着质量为0.2kg的物体A静止在水平转盘上,细绳另一端通过转盘中心的光滑小孔O吊着质量为0.3kg的小球B,A的重心到O点的距离为0.2m,若A与转盘间的最大静摩擦力为2N,为使小球B保持静止,求转盘绕中心O旋转的角速度ω的取值范围.(g=10m/s2)
如图所示,用细绳一端系着质量为0.2kg的物体A静止在水平转盘上,细绳另一端通过转盘中心的光滑小孔O吊着质量为0.3kg的小球B,A的重心到O点的距离为0.2m,若A与转盘间的最大静摩擦力为2N,为使小球B保持静止,求转盘绕中心O旋转的角速度ω的取值范围.(g=10m/s2) 一束光垂直BC面射入如图所示的透明三棱镜中,棱镜折射率n=$\sqrt{2}$,求:
一束光垂直BC面射入如图所示的透明三棱镜中,棱镜折射率n=$\sqrt{2}$,求: