题目内容
(16分)如图所示,质量M = 4.0kg的长木板B静止在光滑的水平地面上,在其右端放一质量m = 1.0kg的小滑块A(可视为质点)。初始时刻,A、B分别以v0 = 2.0m/s向左、向右运动,最后A恰好没有滑离B板。已知A、B之间的动摩擦因数μ = 0.40,取g =10m/s2。求:
⑴ A、B相对运动时的加速度aA和aB的大小与方向;
⑵ A相对地面速度为零时,B相对地面运动已发生的位移x;
⑶木板B的长度l。
⑴aA = 4.0m/s2,方向水平向右 aB = 1.0m/s2,方向水平向左
⑵x = 0.875m ⑶l = 1.6m
解析试题分析:⑴ A、B分别受到大小为μmg的作用,根据牛顿第二定律
对A物体:μmg = maA 1分
则aA =" μg" = 4.0m/s2 1分
方向水平向右 1分
对B物体:μmg = MaB 1分
则aB ="μmg" /M = 1.0m/s2 1分
方向水平向左 1分
⑵ 开始阶段A相对地面向左做匀减速运动,速度为0的过程中所用时间为t1,则
v0 = aAt1,则t1 = v0/aA =" 0.50s" 1分
B相对地面向右做减速运动x = v0t - 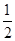 aBt2 =" 0.875m" 1分
aBt2 =" 0.875m" 1分
⑶A向左匀减速运动至速度为零后,相对地面向右做匀加速运动,加速度大小仍为aA = 4.0m/s2;
B板向右仍做匀减速运动,加速度大小仍aB = 1.0m/s2; 1分
当A、B速度相等时,A相对B滑到最左端,恰好不滑出木板,
故木板B的长度为这个全过程中A、B间的相对位移; 1分
在A相对地面速度为零时,B的速度vB = v0 – aBt1 =" 1.5m/s" 1分
设由A速度为零至A、B相等所用时间为t2,则 aAt2 = vB – aBt2,
解得t2 = vB/(aA + aB) = 0.3s;
共同速度v = aAt2 =" 1.2m/s" 1分
A向左运动位移xA = (v0- v)(t1 + t2)/2 =" (2" – 1.2)(0.5 + 0.3)/2 m = 0.32m 1分
B向右运动位移xB = (v0+ v) (t1 + t2)/2 =" (2" + 1.2)(0.5 + 0.3)/2 m 1.28m 1分
B板的长度l = xA + xB = 1.6m 1分
考点:滑动摩擦力 牛顿第二定律

如图所示,小车板面上的物体质量为m=8㎏,它被一根水平方向上拉伸了的弹簧拉住而静止在小车上,这时弹簧的弹力为8N。现沿水平向右的方向对小车施以作用力,使小车由静止开始运动起来,运动中加速度由零逐渐增大到1.5m/s2,随即以1 .5m/s2的加速度做匀加速直线运动。以下说法正确的是 ( )
| A.物体受到的摩擦力一直减小 |
| B.物体与小车始终保持相对静止,弹簧对物体的作用力始终没有发生变化 |
| C.当小车加速度(向右)为0.75 m/s2时,物体不受摩擦力作用 |
| D.小车以1m/s2的加速度向右做匀加速直线运动时,物体受到的摩擦力为8N |

 = 0.20,两圆柱各绕自己的轴线做方向相反的转动,角速度
= 0.20,两圆柱各绕自己的轴线做方向相反的转动,角速度 = 40rad/s,若沿平行于柱轴方向施加推力,推着钢件做速度为v0 = 0.05m/s的匀速运动,推力是多大?设钢件左右受光滑槽限制,不发生横向运动.
= 40rad/s,若沿平行于柱轴方向施加推力,推着钢件做速度为v0 = 0.05m/s的匀速运动,推力是多大?设钢件左右受光滑槽限制,不发生横向运动.



 =3kg,B的质量
=3kg,B的质量 =lkg,A和B间细线的长度L=112.0cm,木板的长度
=lkg,A和B间细线的长度L=112.0cm,木板的长度 =98.0cm,要达实验目的,以上四个量中没有必要测量的是________(用四个物理量的符号表示);
=98.0cm,要达实验目的,以上四个量中没有必要测量的是________(用四个物理量的符号表示);

 mg
mg  mg
mg 