题目内容
设质量相等的甲.乙两颗卫星,分别贴近某星球表面和地球表面,环绕其球心做匀速圆周运动,已知该星球和地球的密度比为1:2,其半径分别为R和r,则(1)甲.乙两颗卫星的加速度之比为______;(2)甲.乙两颗卫星所受的向心力之比为______;(3)甲.乙两颗卫星的线速度之比为______
【答案】分析:根据万有引力提供向心力,可分别得出卫星周期、线速度、向心力、向心加速度与半径关系表达式,进行分析求解.
解答:解:(1)根据万有引力提供向心力得:
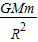 =ma
=ma
a=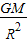 =
=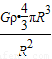 =
= GπρR
GπρR
已知该星球和地球的密度比为1:2,其半径分别为R和r,
所以甲.乙两颗卫星的加速度之比为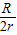
(2)根据牛顿第二定律得:
F向=ma
甲.乙两颗卫星的加速度之比为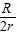 ,甲.乙两颗卫星质量相等,
,甲.乙两颗卫星质量相等,
所以甲.乙两颗卫星所受的向心力之比为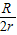
(3)根据万有引力提供向心力得:
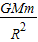 =m
=m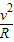
v=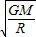 =
=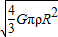
已知该星球和地球的密度比为1:2,其半径分别为R和r,
所以甲.乙两颗卫星的线速度之比为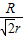
(4)根据圆周运动公式得:
T=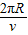
甲.乙两颗卫星的线速度之比为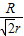
所以甲.乙两颗卫星的周期之比为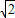 :1.
:1.
故答案为:(1)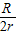 ,(2)
,(2)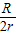 ,(3)
,(3)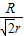 ,(4)
,(4)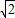 :1.
:1.
点评:对于人造地球卫星问题,常常建立这样模型:卫星绕地球做匀速圆周运动,地球对卫星的万有引力提供卫星的向心力.
解答:解:(1)根据万有引力提供向心力得:
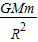 =ma
=maa=
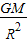 =
=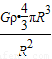 =
= GπρR
GπρR已知该星球和地球的密度比为1:2,其半径分别为R和r,
所以甲.乙两颗卫星的加速度之比为
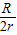
(2)根据牛顿第二定律得:
F向=ma
甲.乙两颗卫星的加速度之比为
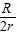 ,甲.乙两颗卫星质量相等,
,甲.乙两颗卫星质量相等,所以甲.乙两颗卫星所受的向心力之比为
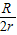
(3)根据万有引力提供向心力得:
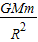 =m
=m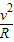
v=
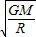 =
=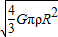
已知该星球和地球的密度比为1:2,其半径分别为R和r,
所以甲.乙两颗卫星的线速度之比为
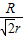
(4)根据圆周运动公式得:
T=
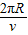
甲.乙两颗卫星的线速度之比为
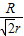
所以甲.乙两颗卫星的周期之比为
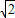 :1.
:1.故答案为:(1)
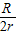 ,(2)
,(2)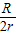 ,(3)
,(3)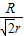 ,(4)
,(4)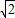 :1.
:1.点评:对于人造地球卫星问题,常常建立这样模型:卫星绕地球做匀速圆周运动,地球对卫星的万有引力提供卫星的向心力.

练习册系列答案
相关题目