题目内容
16. 如图所示为赛车场的一个水平“U”形弯道,转弯处为圆心在O点的半圆,内外半径分别为r和2r.一辆质量为m的赛车通过AB线经弯道到达A'B'线,有如图所示的①②③三条路线,其中路线③是以O'为圆心的半圆,OO'=r.赛车沿圆弧路线行驶时,路面对轮胎的最大径向静摩擦力为Fmax.选择路线,赛车以不打滑的最大速率通过弯道(所选路线内赛车速率不变,发动机功率足够大),则下列说法错误的是( )
如图所示为赛车场的一个水平“U”形弯道,转弯处为圆心在O点的半圆,内外半径分别为r和2r.一辆质量为m的赛车通过AB线经弯道到达A'B'线,有如图所示的①②③三条路线,其中路线③是以O'为圆心的半圆,OO'=r.赛车沿圆弧路线行驶时,路面对轮胎的最大径向静摩擦力为Fmax.选择路线,赛车以不打滑的最大速率通过弯道(所选路线内赛车速率不变,发动机功率足够大),则下列说法错误的是( )| A. | 选择路线①,赛车经过的路程最短 | |
| B. | 选择路线②,赛车的速率最小 | |
| C. | 选择路线③,赛车所用时间最短 | |
| D. | ①②③三条路线的圆弧上,赛车的向心加速度大小相等 |
分析 根据几何关系得出路程的大小从而进行比较.根据最大静摩擦力,结合牛顿第二定律得出最大速率,从而比较运动的时间.根据向心加速度公式比较三段路线的向心加速度关系.
解答 解:A、选择路线①,经历的路程s1=2r+πr,选择路线②,经历的路程s2=2πr+2r,选择路线③,经历的路程s3=2πr,可知选择路线①,赛车经过的路程最短,故A正确.
B、根据Fmax=$\frac{m{v}^{2}}{r}$得,v=$\sqrt{\frac{{F}_{max}r}{m}}$知,选择路线①,轨道半径最小,则速率最小,故B错误.
C、根据v=$\sqrt{\frac{{F}_{max}r}{m}}$可知,通过①、②、③三条路线的最大速率之比为1:$\sqrt{2}$:$\sqrt{2}$,根据t=$\frac{s}{v}$,由三段路程可知,选择路线③,赛车所用时间最短,故C正确.
D、根据a=$\frac{{v}^{2}}{r}$知,因为最大速率之比为1:$\sqrt{2}$:$\sqrt{2}$,半径之比为1:2:2,则三条路线上,赛车的向心加速度大小相等.故D正确.
本题选错误的,故选:B.
点评 本题考查了圆周运动向心加速度、向心力在实际生活中的运用,知道汽车做圆周运动,靠静摩擦力提供向心力,抓住最大静摩擦力相等求出最大速率之比是关键

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
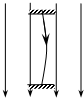
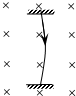
5. 以一定的初速度将甲、乙、丙三个小球向右水平抛出,落在右侧的竖直墙上,轨迹如图.其中甲和丙落在同一点.(不计空气阻力)则关于它们的初速度v的关系正确的是( )
以一定的初速度将甲、乙、丙三个小球向右水平抛出,落在右侧的竖直墙上,轨迹如图.其中甲和丙落在同一点.(不计空气阻力)则关于它们的初速度v的关系正确的是( )
 以一定的初速度将甲、乙、丙三个小球向右水平抛出,落在右侧的竖直墙上,轨迹如图.其中甲和丙落在同一点.(不计空气阻力)则关于它们的初速度v的关系正确的是( )
以一定的初速度将甲、乙、丙三个小球向右水平抛出,落在右侧的竖直墙上,轨迹如图.其中甲和丙落在同一点.(不计空气阻力)则关于它们的初速度v的关系正确的是( )| A. | v甲>v乙>v丙 | B. | v甲=v乙<v丙 | C. | v乙<v甲<v丙 | D. | v甲=v丙>v乙 |
11.把两个相同的金属小球相互靠近时,发现它们相互吸引,现将两个小球接触一下,再分开一小段距离,发现它们相互排斥.则下列说法正确的是( )
| A. | 两球原来一定带有不等量异种电荷 | B. | 两球原来带有同种电荷 | ||
| C. | 可能两球中原来只有一个带电 | D. | 现在两球所带电荷量肯定不相等 |
1.蹦极(Bungee Junping)是一项非常刺激的户外休闲活动.设某次跳跃者在蹦极运动场地把长为15m橡皮条一端固定,另一端绑在踝关节处,然后从离地40m高处跳下,跳跃者在空中能够享受到几秒钟的“自由落体”.当人体落到离地面高度为6m时,跳跃者在橡皮绳弹力的作用下开始往上升,假如跳跃者第一次被拉起能达到的最高点在起跳点下方10m处.若跳跃者可视为质点,则从跳跃者起跳到第一次到达最高点的过程中,跳跃者通过的路程和位移大小分别是( )
| A. | 70m、15m | B. | 58m、10m | C. | 43m、10m | D. | 58m、24m |
8. 三颗人造卫星A、B、C绕地球做匀速圆周运动.如图所示,已知mA=mB<mC,则对于三颗卫星,正确的是( )
三颗人造卫星A、B、C绕地球做匀速圆周运动.如图所示,已知mA=mB<mC,则对于三颗卫星,正确的是( )
 三颗人造卫星A、B、C绕地球做匀速圆周运动.如图所示,已知mA=mB<mC,则对于三颗卫星,正确的是( )
三颗人造卫星A、B、C绕地球做匀速圆周运动.如图所示,已知mA=mB<mC,则对于三颗卫星,正确的是( )| A. | 运行线速度关系为vA<vB=vC | |
| B. | 运行周期关系为 TA=TB<TC | |
| C. | 向心力大小关系为 FA=FB>FC | |
| D. | 运行半径与周期关系为$\frac{{{R}_{A}}^{3}}{{{T}_{A}}^{2}}$=$\frac{{{R}_{B}}^{3}}{{{T}_{B}}^{2}}$=$\frac{{{R}_{C}}^{3}}{{{T}_{C}}^{2}}$ |
5.物理学中有多种研究方法,有关研究方法的叙述错误的是( )
| A. | 在伽利略之前的学者们总是通过思辩性的论战决定谁是谁非,是他首先采用了以实验检验猜想和假设的科学方法 | |
| B. | 探究加速度与力、质量之间的定量关系,可以在质量一定的情况下,探究物体的加速度与力的关系;再在物体受力一定的情况下,探究物体的加速度与质量的关系,最后归纳出加速度与力、质量之间的关系.这是物理学中常用的控制变量的研究方法 | |
| C. | 探究作用力与反作用力关系时可以用传感器连在计算机上直接显示力的大小随时间的变化情况,用图象的方法来研究 | |
| D. | 如果电场线与等势面不垂直,那么电场强度就有一个沿着等势面的分量,在等势面上移动电荷时静电力就要做功,这里用的逻辑方法是归纳法 |


 两个相同的白炽灯L1和L2接到如图所示的电路中,灯L1与电容器串联,灯L2与电感线圈串联,当a、b间接交变电压,电路稳定后,保持电压不变只增加交变电压的频率,则L1亮度变亮,L2亮度变暗(填“变亮”或“变亮”“不变”)
两个相同的白炽灯L1和L2接到如图所示的电路中,灯L1与电容器串联,灯L2与电感线圈串联,当a、b间接交变电压,电路稳定后,保持电压不变只增加交变电压的频率,则L1亮度变亮,L2亮度变暗(填“变亮”或“变亮”“不变”)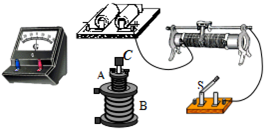 在“研究电磁感应现象”的实验中,所用的器材如图所示.
在“研究电磁感应现象”的实验中,所用的器材如图所示.