Question

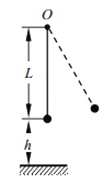
【题目】如图所示，一轻绳连着一小球，悬挂于O点，现把小球拉开一角度后静止释放。设小球质量m=3kg，绳长L=4m，小球运动的最低点离地高度h=5m。

（1）若小球通过最低点的速度大小为v=2m/s，求此时绳的拉力大小；

（2）若轻绳能够承受的最大拉力为78N，求允许小球通过最低点的最大速率；

（3）若以（2）问的最大速率通过最低点时，轻绳恰好断裂，小球抛出，求小球平抛的水平位移大小。

Answer 1

【答案】（1）33N；（2）8m/s；（3）8m

【解析】

（1）质点在最低点受到的拉力与重力提供向心力，则：

，

代入数据解得：

F=33N

（2）小球下摆到B点时，绳的拉力和重力提供向心力，

由牛顿第二定律的：

，

代入数据解得：

vm=8m/s

（3）绳子断后，小球做平抛运动，运动时间为t，

竖直方向：h=gt2，

水平方向，DC间距离：x=vmt，

代入数据解得：x=8m；

答：（1）若小球通过最低点的速度大小为v=2m/s，此时绳的拉力大小为33N；

（2）若轻绳能够承受的最大拉力为78N，允许小球通过最低点的最大速率为8m/s；

（3）若以（2）问的最大速率通过最低点时，轻绳恰好断裂，小球抛出，小球平抛的水平位移大小为8m。