题目内容
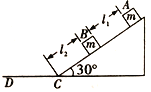
【题目】如图所示,质量均为m的物体A、B放在倾角θ=30°的斜面上,已知A与斜面及水平面间的动摩擦因数μ1=![]() ,B与斜面及水平面间的动摩擦因数μ2=
,B与斜面及水平面间的动摩擦因数μ2=![]() ,A、B两物体之间的距离l1=1m,B到斜面底端的距离为l2,最大静摩擦力等于滑动摩擦力。现将A、B两物体同时由静止开始释放,它们间的碰撞为弹性碰撞,g取10m/s2。
,A、B两物体之间的距离l1=1m,B到斜面底端的距离为l2,最大静摩擦力等于滑动摩擦力。现将A、B两物体同时由静止开始释放,它们间的碰撞为弹性碰撞,g取10m/s2。
(1)求A、B两物体经过多长时间第一次相遇;
(2)若l2=0.8m,则物体A、B最终停在何处?
【答案】(1) ![]() (2) 物体A静止在C处,物体B停的位置距C点的距离
(2) 物体A静止在C处,物体B停的位置距C点的距离![]()
【解析】
(1)将两物体由静止释放后,对物体A进行受力分析有
![]()
解得:
![]()
对物体B进行受力分析,有:
![]()
所以物体B静止在斜面上
设A、B两物体经过时间![]() 第一次相遇,则:
第一次相遇,则:
![]()
解得:
![]()
(2)A、B两物体相遇后发生弹性碰撞,设碰撞前物体A的速度为![]() ,则:
,则:
![]()
碰撞后物体A的速度为![]() ,物体B的速度为
,物体B的速度为![]() ,由于碰撞过程中动量守恒、能量守恒,则
,由于碰撞过程中动量守恒、能量守恒,则
![]()
![]()
解得:
![]()
![]()
此后物体B做减速运动,物体A再次做初速度为零的匀加速运动,物体B的加速度大小:
![]()
减速到零所用的时间
![]()
运动的位移
![]()
此时物体A运动的位移
![]()
所以AB未发生碰撞,当物体A与物体B发生第二次碰撞前,物体A的速度
![]()
同理可知,碰撞后物体A静止在C处,物体B的速度
![]()
此后物体B沿水平面做减速运动,物体B的加速度大小
![]()
最终物体B停的位置距C点的距离
![]()

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目