题目内容
18.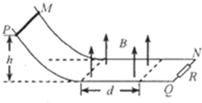 如图所示,MN和PQ是电阻不计的平行金属导轨,其间距为L,导轨弯曲部分光滑,平直部分粗糙,二者平滑连接.右端接一个阻值为R的定值电阻.平直部分导轨左边区域有宽度为d、方向竖直向上、磁感应强度大小为B的匀强磁场.质量为m、电阻也为R的金属棒从高度为h处静止释放,到达磁场右边界处恰好停止.已知金属棒与平直部分导轨间的动摩擦因数为μ,金属棒与导轨间接触良好.则金属棒穿过磁场区域的过程中( )
如图所示,MN和PQ是电阻不计的平行金属导轨,其间距为L,导轨弯曲部分光滑,平直部分粗糙,二者平滑连接.右端接一个阻值为R的定值电阻.平直部分导轨左边区域有宽度为d、方向竖直向上、磁感应强度大小为B的匀强磁场.质量为m、电阻也为R的金属棒从高度为h处静止释放,到达磁场右边界处恰好停止.已知金属棒与平直部分导轨间的动摩擦因数为μ,金属棒与导轨间接触良好.则金属棒穿过磁场区域的过程中( )| A. | 流过定值电阻的电流方向是N→Q | |
| B. | 通过金属棒的电荷量为$\frac{BdL}{2R}$ | |
| C. | 金属棒滑过连接处时的速度大于$\sqrt{2gh}$ | |
| D. | 金属棒产生的焦耳热为$\frac{1}{2}$(mgh-μmgd) |
分析 由右手定则可以判断出感应电流的方向;
应用法拉第电磁感应定律、欧姆定律、电流定义式可以求出通过电阻的电荷量;
克服安培力做功转化为焦耳热,由动能定理(或能量守恒定律)可以求出克服安培力做功,导体棒产生的焦耳热.
解答 解:A、金属棒下滑到低端时速度向右,而且磁场竖直向上,根据右手定则可以知道流过定值电阻的电流方向是Q→N,故选项A错误;
B、根据法拉第电磁感应定律,通过金属棒的电荷量为:q=$\frac{E}{2R}△t$=$\frac{△∅}{△t•2R}△t$=$\frac{BLd}{2R}$,故B正确;
C、根据能量守恒定律可知,因存在摩擦阻力做功,则导致金属棒滑过连接处时的速度小于$\sqrt{2gh}$,故C错误;
D、根据动能定理则:mgh-μmgd-W安=0,则克服安培力所做的功为W=mgh-μmgd;电路中产生的焦耳热等于客服安培力做功,所以金属棒产生的焦耳热为$\frac{1}{2}(mgh-μmgd)$,故D正确.
故选:BD.
点评 本题综合考查了判断感应电流方向、法拉第电磁感应定律、闭合电路欧姆定律等,综合性较强,对学生能力要求较高,需加强这方面的训练.

练习册系列答案
相关题目
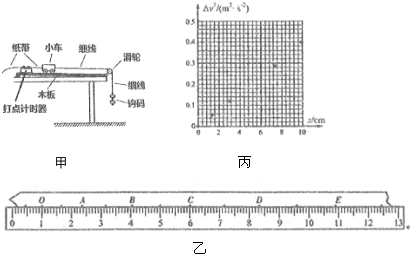
6.某同学采用如图甲所示的装置研究匀变速直线运动.打点计时器工作频率为50Hz.
该同学的操作步骤如下:
a.将木板的左端垫起,平衡小车的摩擦力;
b.在小车中放入砝码,纸带穿过打点计时器,连在小车后端,用细线连接小车和钩码;
c.将小车停在打点计时器附近,接通电源,释放小车,小车拖地纸带,打点计时器在纸带上打下一系列的点,断开电源;
d.改变钩码或小车中砝码的质量,更换纸带,重复b、c的操作.
(1)设钩码质量为m1,砝码和小车总质量为m2,重力加速度为g,则小车的加速度为:a=$\frac{{m}_{1}}{{m}_{2}+{m}_{1}}$(用题中所给字母表示);
(2)图乙是某次实验中得到的一条纸带,在纸带上取计数点O、A、B、C、D和E,用最小刻度是毫米的刻度尺进行测量,读出各计数点对应的刻度x,通过计算得到各计数点到O的距离s以及对应时刻小车的瞬时速度v.某同学不小心将计数点C的数据弄模糊了,请你将C点对应的数据填在表中的相应位置.
(3)实验小组通过绘制△v2-s图线来分析运动规律(其中△v2=v2-v02,v是各计数点对应时刻小车的瞬时速度,v0是O点对应时刻小车的瞬时速度).他们根据实验数据在图丙中标出了O、A、B、C、D、E对应的坐标点,请你在图丙中画出△v2-s图线.
(4)绘制的△v2-s图线的斜率k=$\frac{2{m}_{1}}{{m}_{2}+{m}_{1}}$(用题中所给字母表示).若发现该斜率大于理论值,其原因可能是木板的左侧垫的过高.
该同学的操作步骤如下:
a.将木板的左端垫起,平衡小车的摩擦力;
b.在小车中放入砝码,纸带穿过打点计时器,连在小车后端,用细线连接小车和钩码;
c.将小车停在打点计时器附近,接通电源,释放小车,小车拖地纸带,打点计时器在纸带上打下一系列的点,断开电源;
d.改变钩码或小车中砝码的质量,更换纸带,重复b、c的操作.
(1)设钩码质量为m1,砝码和小车总质量为m2,重力加速度为g,则小车的加速度为:a=$\frac{{m}_{1}}{{m}_{2}+{m}_{1}}$(用题中所给字母表示);
(2)图乙是某次实验中得到的一条纸带,在纸带上取计数点O、A、B、C、D和E,用最小刻度是毫米的刻度尺进行测量,读出各计数点对应的刻度x,通过计算得到各计数点到O的距离s以及对应时刻小车的瞬时速度v.某同学不小心将计数点C的数据弄模糊了,请你将C点对应的数据填在表中的相应位置.
| 计数点 | x/cm | s/cm | v/(m•s)-1 |
| O | 1.00 | 0.30 | |
| A | 2.34 | 1.34 | 0.38 |
| B | 4.04 | 3.04 | 0.46 |
| C | 6.00 | 5.00 | 0.54 |
| D | 8.33 | 7.33 | 0.61 |
| E | 10.90 | 9.90 | 0.70 |
(4)绘制的△v2-s图线的斜率k=$\frac{2{m}_{1}}{{m}_{2}+{m}_{1}}$(用题中所给字母表示).若发现该斜率大于理论值,其原因可能是木板的左侧垫的过高.

13.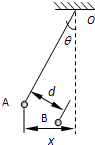 某老师用图示装置探究库仑力与电荷量的关系.A、B是可视为点电荷的两带电小球,用绝缘细线将A悬挂,实验中在改变电荷量时,移动B并保持A、B连线与细线垂直.用Q和q表示A、B的电荷量,d表示A、B间的距离,θ(θ不是很小)表示细线与竖直方向的夹角,x表示A偏离O点的水平距离.实验中( )
某老师用图示装置探究库仑力与电荷量的关系.A、B是可视为点电荷的两带电小球,用绝缘细线将A悬挂,实验中在改变电荷量时,移动B并保持A、B连线与细线垂直.用Q和q表示A、B的电荷量,d表示A、B间的距离,θ(θ不是很小)表示细线与竖直方向的夹角,x表示A偏离O点的水平距离.实验中( )
 某老师用图示装置探究库仑力与电荷量的关系.A、B是可视为点电荷的两带电小球,用绝缘细线将A悬挂,实验中在改变电荷量时,移动B并保持A、B连线与细线垂直.用Q和q表示A、B的电荷量,d表示A、B间的距离,θ(θ不是很小)表示细线与竖直方向的夹角,x表示A偏离O点的水平距离.实验中( )
某老师用图示装置探究库仑力与电荷量的关系.A、B是可视为点电荷的两带电小球,用绝缘细线将A悬挂,实验中在改变电荷量时,移动B并保持A、B连线与细线垂直.用Q和q表示A、B的电荷量,d表示A、B间的距离,θ(θ不是很小)表示细线与竖直方向的夹角,x表示A偏离O点的水平距离.实验中( )| A. | d应保持不变 | B. | B的位置在同一圆弧上 | ||
| C. | x与电荷量乘积Qq成正比 | D. | tanθ与A、B间库仑力成正比 |
3.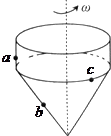 如图所示是一个玩具陀螺.A.b和c是陀螺表面上的三个点.当陀螺绕垂直于地面的轴线以角速度ω稳定旋转时( )
如图所示是一个玩具陀螺.A.b和c是陀螺表面上的三个点.当陀螺绕垂直于地面的轴线以角速度ω稳定旋转时( )
 如图所示是一个玩具陀螺.A.b和c是陀螺表面上的三个点.当陀螺绕垂直于地面的轴线以角速度ω稳定旋转时( )
如图所示是一个玩具陀螺.A.b和c是陀螺表面上的三个点.当陀螺绕垂直于地面的轴线以角速度ω稳定旋转时( )| A. | a、b的角速度比c的大 | B. | a、b、c三点的角速度相等 | ||
| C. | a、b、c三点的线速度大小相等 | D. | a、b的线速度比c的小 |
10.音箱装饰布网既美观又能阻止灰尘进入音箱内部,但是它又有不利的一面,对于音箱发出的声音来说,布网就成了障碍物,它障碍了声音的传播,造成了声音失真,有的生产厂家就把装饰布网安装了子母扣,这样听音乐时就可以把布网卸下来,从而获得高保真的听觉效果,听同样的音乐不卸下布网和卸下布网相比较,你认为声音损失掉的主要是( )
| A. | 高频部分 | B. | 低频部分 | C. | 中频部分 | D. | 中频和低频 |
7. 如图所示,一个球从高处自由下落到达A点与一个轻质弹簧相撞,弹簧被压缩.取地面为重力势能的参考平面,从球与弹簧接触,到弹簧被压缩到最短的过程中,关于球的动能、重力势能、弹簧的弹性势能的说法中正确的是( )
如图所示,一个球从高处自由下落到达A点与一个轻质弹簧相撞,弹簧被压缩.取地面为重力势能的参考平面,从球与弹簧接触,到弹簧被压缩到最短的过程中,关于球的动能、重力势能、弹簧的弹性势能的说法中正确的是( )
 如图所示,一个球从高处自由下落到达A点与一个轻质弹簧相撞,弹簧被压缩.取地面为重力势能的参考平面,从球与弹簧接触,到弹簧被压缩到最短的过程中,关于球的动能、重力势能、弹簧的弹性势能的说法中正确的是( )
如图所示,一个球从高处自由下落到达A点与一个轻质弹簧相撞,弹簧被压缩.取地面为重力势能的参考平面,从球与弹簧接触,到弹簧被压缩到最短的过程中,关于球的动能、重力势能、弹簧的弹性势能的说法中正确的是( )| A. | 球的动能先增大后减小 | |
| B. | 球的动能一直在减小 | |
| C. | 球的动能和重力势能之和始终逐渐减小 | |
| D. | 球的重力势能和弹簧的弹性势能之和先减小后增大 |
8. a、b、c三个完全相同的带正电的微粒(不计重力)由同一点同时垂直场强方向进入偏转电场,其轨迹如图所示,其中b恰好飞出电场,则以下说法正确的是( )
a、b、c三个完全相同的带正电的微粒(不计重力)由同一点同时垂直场强方向进入偏转电场,其轨迹如图所示,其中b恰好飞出电场,则以下说法正确的是( )
 a、b、c三个完全相同的带正电的微粒(不计重力)由同一点同时垂直场强方向进入偏转电场,其轨迹如图所示,其中b恰好飞出电场,则以下说法正确的是( )
a、b、c三个完全相同的带正电的微粒(不计重力)由同一点同时垂直场强方向进入偏转电场,其轨迹如图所示,其中b恰好飞出电场,则以下说法正确的是( )| A. | 在b飞离电场的同时,a刚好打在负极板上 | |
| B. | b和c同时飞离电场 | |
| C. | 进入电场时,c的速度最大,a的速度最小 | |
| D. | 动能的增量相比,c的最小,a和b的一样大 |
 某列波在t=0时刻的波形图如图所示,此时质点P正向y轴正方向运动,经0.1s第一次达到波峰位置,求:
某列波在t=0时刻的波形图如图所示,此时质点P正向y轴正方向运动,经0.1s第一次达到波峰位置,求: 如图所示,一质量为m、带电量为q的小球,用绝缘细线悬挂在水平向右的匀强电场中,静止时悬线向左与竖直方向成θ角,重力加速度为g.判断小球带负电荷(正或负),电场强度E=$\frac{mgtanθ}{q}$.
如图所示,一质量为m、带电量为q的小球,用绝缘细线悬挂在水平向右的匀强电场中,静止时悬线向左与竖直方向成θ角,重力加速度为g.判断小球带负电荷(正或负),电场强度E=$\frac{mgtanθ}{q}$.