题目内容
9．
如图所示，一质量为m、带电量为q的小球，用绝缘细线悬挂在水平向右的匀强电场中，静止时悬线向左与竖直方向成θ角，重力加速度为g．判断小球带负电荷（正或负），电场强度E=$\frac{mgtanθ}{q}$．
分析 对小球受力分析，根据共点力平衡得出电场力的方向，从而确定小球的电性，根据共点力平衡得出电场力的大小，从而求出电场强度．
解答 解：根据小球的受力分析知，电场力水平向左，知小球带负电．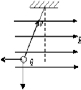
根据共点力平衡得，F=qE，
又F=mgtanθ，
所以E=$\frac{mgtanθ}{q}$．
故答案为：负；$\frac{mgtanθ}{q}$
点评 解决本题的关键能够正确地受力分析，运用共点力平衡进行求解．
练习册系列答案
相关题目
12．一列简谐横波沿x轴传播，t=0时刻的波形如图甲所示，A、P和Q是介质中的三个质点，A的振动图象如图乙所示．下列判断正确的是（ ）
| A． | 该波的传播速度是2.5m/s | |
| B． | 该波沿x轴正方向传播 | |
| C． | 从0～0.4s，P通过的路程为4m | |
| D． | 从t=0时刻开始，P将比Q先回到平衡位置 |
如图，水平粗糙轨道AB与半圆形光滑的竖直圆轨道BC相连，B点与C点的连线沿竖直方向，AB段长为L，圆轨道的半径为R．一个小滑块以初速度vo从A点开始沿轨道滑动，已知它运动到C点时对轨道的压力大小恰好等于其重力．求：
如图所示，空中有四个点电荷A、B、C、D，A和B所带电荷量为+Q，C和D所带电荷量为-Q，A、B固定不动，相距为L，AB连线水平，CD连线与AB连线相交于O点，且互相垂直平分，C、D相距为L，且以相同的角速度在垂直AB连线的竖直面内绕O点作匀速圆周运动，C、D质量均为m，不计重力，静电力常量为k，求：
4．
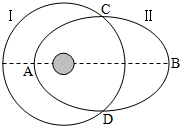如图为两颗人造卫星绕地球运动的轨道示意图，Ⅰ为圆轨道，Ⅱ为椭圆轨道，AB为椭圆的长轴，两轨道和地心都在同一平面内，C、D为两轨道交点．己知轨道Ⅱ上的卫星运动到C点时速度方向与AB平行，则下列说法正确的是（ ）
如图为两颗人造卫星绕地球运动的轨道示意图，Ⅰ为圆轨道，Ⅱ为椭圆轨道，AB为椭圆的长轴，两轨道和地心都在同一平面内，C、D为两轨道交点．己知轨道Ⅱ上的卫星运动到C点时速度方向与AB平行，则下列说法正确的是（ ）| A． | 两个轨道上的卫星运动到C点时的加速度不相同 | |
| B． | 两个轨道上的卫星运动到C点时的向心加速度大小相等 | |
| C． | 若卫星在Ⅰ轨道的速率为v1，卫星在Ⅱ轨道B点的速率为v2，则v1＜v2 | |
| D． | 两颗卫星的运动周期相同 |
14．已知月球绕地球公转的周期为T，地球半径为R，地球表面的重力加速度为g，则月球绕地球公转的线速度大小为（ ）
| A． | $\root{3}{\frac{2πg{R}^{2}}{T}}$ | B． | $\root{3}{\frac{πg{R}^{2}}{2T}}$ | C． | 2$\root{3}{\frac{πg{R}^{2}}{T}}$ | D． | $\frac{1}{2}$$\root{3}{\frac{πg{R}^{2}}{T}}$ |
如图所示，竖直平面内的直角坐标系中，在y＞0区域内，有沿y轴负方向的匀强电场；在y＜0的区域内，有沿y轴正方向、大小和y＞0区域相等的匀强电场、以及垂直纸面的匀强磁场（图中没有标出）．一质量为m、电荷量为+q的微粒从y轴上P点，以沿x轴正方向、大小为2$\sqrt{gl}$的初速度开始运动．当微粒第一次穿过x轴时，恰好到达Q点；当微粒第二次穿过x轴时，恰好到达坐标原点；当微粒第三次穿过x轴时，恰好到达S点．已知P、Q两点到坐标原点的距离分别为l、2l，重力加速度为g．求：
18．
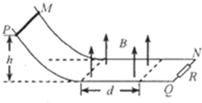如图所示，MN和PQ是电阻不计的平行金属导轨，其间距为L，导轨弯曲部分光滑，平直部分粗糙，二者平滑连接．右端接一个阻值为R的定值电阻．平直部分导轨左边区域有宽度为d、方向竖直向上、磁感应强度大小为B的匀强磁场．质量为m、电阻也为R的金属棒从高度为h处静止释放，到达磁场右边界处恰好停止．已知金属棒与平直部分导轨间的动摩擦因数为μ，金属棒与导轨间接触良好．则金属棒穿过磁场区域的过程中（ ）
如图所示，MN和PQ是电阻不计的平行金属导轨，其间距为L，导轨弯曲部分光滑，平直部分粗糙，二者平滑连接．右端接一个阻值为R的定值电阻．平直部分导轨左边区域有宽度为d、方向竖直向上、磁感应强度大小为B的匀强磁场．质量为m、电阻也为R的金属棒从高度为h处静止释放，到达磁场右边界处恰好停止．已知金属棒与平直部分导轨间的动摩擦因数为μ，金属棒与导轨间接触良好．则金属棒穿过磁场区域的过程中（ ）| A． | 流过定值电阻的电流方向是N→Q | |
| B． | 通过金属棒的电荷量为$\frac{BdL}{2R}$ | |
| C． | 金属棒滑过连接处时的速度大于$\sqrt{2gh}$ | |
| D． | 金属棒产生的焦耳热为$\frac{1}{2}$（mgh-μmgd） |
