题目内容
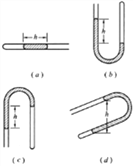
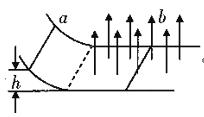
【题目】如图所示,质量为m的导体棒a从h高处由静止起沿足够长的光滑导电轨道滑下,另一质量为2m的导体棒b静止在宽为L的光滑水平导轨上,在水平轨道区域有垂直于轨道平面向上的匀强磁场,磁感应强度为B,a、b导体棒不会相碰,重力加速度取g,则a、b导体棒的最终的共同速度为__________,回路中最多能产生焦耳热为__________。
【答案】![]()
![]()
【解析】
a先加速下滑,进入磁场后切割磁感线,产生感应电动势和感应电流,受到向左的安培力而做减速运动,b在安培力作用下向右加速运动,也切割磁感线产生感应电动势,此感应电动势与a的感应电动势方向相反,整个回路总的电动势减小,感应电流减小,两棒所受的安培力减小,当两棒的速度相等时,电路中不再产生感应电流,两棒不受安培力,将一起做匀速运动,达到稳定状态。以两棒组成的系统为研究对象,满足动量守恒,据动量守恒定律求解即可;当两棒最终一-起做匀速运动时,回路中不再产生焦耳热,根据能量守恒定律求解即可。
第一空.a从h高处由静止滑到水平导轨处,由动能定理得:
![]() ,
,
解得:![]()
a进入磁场后,a棒减速,b棒加速,最终速度相等,a、b系统水平方向合外力为零。
设水平向右为正方向,由动量守恒定律得:
![]() ,
,
解得,最终速度:![]() ;
;
第二空.整个过程,对系统,由能量守恒定律得:
![]()
解得:![]() 。
。

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目