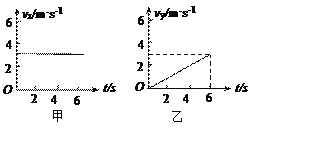题目内容
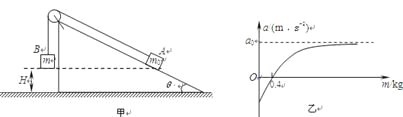
【题目】如图甲所示，水平面上固定一个倾角为θ的光滑足够长斜面，斜面顶端有一光滑的轻质定滑轮，跨过定滑轮的轻细绳两端分别连接物块A和B（可看作质点），开始A、B离水平地面的高度Ｈ＝0.5m，A的质量m0=0.8kg。当B的质量m连续变化时，可以得到A的加速度变化图线如乙图所示，图中虚线为渐近线，设加速度沿斜面向上的方向为正方向，不计空气阻力，重力加速度为g取10m/s2。求：
⑴斜面的倾角θ；
⑵图乙中a0值；
⑶若m=1.2kg，由静止同时释放A、B后，A上升离水平地面的最大高度（设B着地后不反弹）。
【答案】（1）θ=
（2）a0= g（3）
【解析】试题分析：⑴当m=0.4kg时，a=0，所以 F=mg m0gsinθ=F （2分）
解得 θ=（1分）
⑵ mg-F=ma （1分）
F -m0gsinθ=m0a （1分）
得： 
（2分）
当mà∞时，a0= g （1分）
⑶AB的加速度大小
=4m/s2（2分）
B着地时的速度：
（2分）
接着A作匀减速直线运动，到速度为零时到达最高点，
由机械能守恒得上升的高度
得：
（2分）
A距离水平面最大高度
（2分）
练习册系列答案
同步练习河南大学出版社系列答案
同步练习西南师范大学出版社系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目
