Question

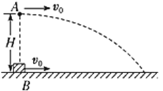
【题目】如图所示，从倾角为θ的斜面上的A点以初速度v0水平抛出一个物体，物体落在斜面上的B点，不计空气阻力．求：

(1)抛出后经多长时间物体与斜面间距离最大？

(2)A、B间的距离为多少？

Answer 1

【答案】(1) (2)

【解析】

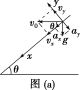
法一：(1) 以抛出点为坐标原点，沿斜面方向为轴，垂直于斜面方向为轴，建立坐标系，如图(a)所示，则有：

物体沿斜面方向做初速度为、加速度为的匀加速直线运动，垂直于斜面方向做初速度为、加速度为的匀减速直线运动，类似于竖直上抛运动

物体与斜面间距离最大：

(2)当时，物体离斜面最远，由对称性可知总飞行时间：

、间距离：

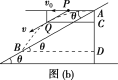
法二：(1) 如图(b)所示，当速度方向与斜面平行时，离斜面最远，的切线反向延长与交点为此时横坐标的中点，

则有：

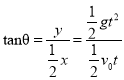
解得：

(2)在竖直方向则有：

而：

则有：

、间距离：

法三：(1)设物体运动到点离斜面最远，所用时间为，将分解成和，如图(c)所示，则由：

解得：

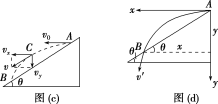
(2)设由到所用时间为，水平位移为，竖直位移为，如图(d)所示，由图可得：

联立解得：

则有：

因此、间距离：