题目内容
【题目】某游乐园的大型 “跳楼机”游戏,以惊险刺激深受年轻人的欢迎。某次游戏中,质量m=50kg的小明同学坐在载人平台上,并系好安全带、锁好安全杆。游戏的过程简化为巨型升降机将平台拉升100m高度,然后由静止开始下落,在忽略空气和台架对平台阻力的情况下,该运动可近似看作自由落体运动。下落h1=80 m时,制动系统启动,使平台均匀减速,再下落h2=20m时刚好停止运动。取g=10m/s2,求:

(1)下落的过程中小明运动速度的最大值vm;
(2)当平台落到离地面15m高的位置时,小明对跳楼机作用力F的大小;
(3)在全部下落过程中,跳楼机对小明做的功W。
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】解:(1)由vm2![]()
有 vm=40m/s
(2)减速下落过程中加速度大小![]()
解得a2=40m/s2
根据牛顿第二定律 F- mg= ma2
解得F=2500 N
根据牛顿第三定律,小明对系统作用力的大小F为2500N
(3)加速下落段,小明处于完全失重状态,系统对小明的作用力为零。
对小明W1=0
在减速阶段,系统对小明做功W2=-FN![]() h2= -5
h2= -5![]() 104J
104J
WFN=W1+W2=-5![]() 104J
104J

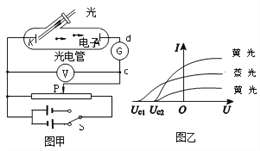
【题目】某同学用如图所示装置“研究物体的加速度与外力关系”,他将光电门固定在气垫轨道上的某点B处,调节气垫导轨水平后,用重力为F的钩码,经绕过滑轮的细线拉滑块,每次滑块从同一位置A由静止释放,测出遮光条通过光电门的时间t。改变钩码个数,重复上述实验。记录的数据及相关计算如下表。


实验次数 | 1 | 2 | 3 | 4 | 5 |
F/N | 0.05 | 0.10 | 0.15 | 0.20 | 0.25 |
t/(m.s) | 40.4 | 28.6 | 23.3 | 20.2 | 18.1 |
t2/(m.s)2 | 1632.2 | 818.0 | 542.9 | 408.0 | 327.6 |
1/t2(×10-4ms-2) | 6.1 | 12.2 | 18.4 | 24.4 | 30.5 |
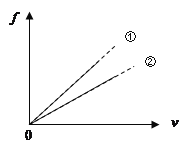
①为便于分析F与t的关系,在坐标纸上作出如图所示的图线,图线为__________的关系图象
A.F-t, B.F-t2 C.F-![]()
②结合表格中数据及图线特点,算出图线的斜率k=_________ 。
③设AB间的距离为s,遮光条的宽度为d,由图线的斜率可求得滑块的质量为M为__________。