Question

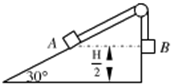如图，倾角为30⁰的斜面高为H，顶端有一小滑轮，物块A和B的质量分别为m₁和m₂，通过轻绳连接，不计一切摩擦．开始时两物块都位于离地面高为H/2的位置，由静止释放两物块后，若物块A恰好能到达斜面顶端，求：
（1）释放瞬间物块A的加速度是多大？
（2）m₁和m₂之比？．

Answer 1

分析：（1）分别以A、B为研究对象列牛顿第二定律方程，解方程组求出加速度大小；
（2）B落地后分别求出A、B的加速度大小，结合速度位移公式表示出A的位移且大小

1

2

H求出二者质量之比．

解答：解：（1）释放瞬间，以A为研究对象：T-m₁gsinθ=m₁a₁
以B为研究对象：m₂g-T=m₂a₁
得：a1=

m2g-m1gsinθ

m1+m2

（2）B从释放到落地，位移：s₁=

1

2

H，v²=2a₁s₁
斜面上半部分长为H，此后A还需上滑s₂=

1

2

H才能到达斜面顶端
以A为研究对象：m₁gsinθ=m₁a₂
到达顶端速度为0，则：v²=2a₂s₂ 
联立求得：m₁：m₂=1：2
答：（1）释放瞬间物块A的加速度是a1=

m2g-m1gsinθ

m1+m2

．
（2）m₁和m₂之比为1：2．

点评：分析清楚物体的运动过程，应用牛顿第二定律和运动学公式求解，也可以应用机械能守恒定律、动能定理解题，可以尝试．