题目内容
 如图所示,匝数为100、面积为0.01m2的线圈,处于磁感应强度B1为
如图所示,匝数为100、面积为0.01m2的线圈,处于磁感应强度B1为| 1 |
| π |
分析:根据Em=NB1Sω求出最大电动势,进而求出有效值,导体棒MN的稳定速度时有F=mgsinθ+B2I′L,此时的电流I′=
=
,根据能量守恒求出电动机的输出功率P出=IU-I2r,则F=
,联立求出稳定速度v.
| E |
| R |
| B2Lv |
| R |
| P出 |
| v |
解答:解:线圈转动过程中电动势的最大值为:
Em=NB1Sω=NB1S?2πn=100×
×0.01×2π×5=10V
解得:E=
=5
V
棒达到稳定速度时,电动机的电流为:I=1A
电动机的输出功率P出=IU-I2r
又P出=Fv
而棒产生的感应电流I′=
=
稳定时棒处于平衡状态,故有:
F=mgsinθ+B2I′L
由以上各式代入数值,得棒的稳定速度为:v=2m/s.
故选:B
Em=NB1Sω=NB1S?2πn=100×
| 1 |
| π |
解得:E=
| Em | ||
|
| 2 |
棒达到稳定速度时,电动机的电流为:I=1A
电动机的输出功率P出=IU-I2r
又P出=Fv
而棒产生的感应电流I′=
| E |
| R |
| B2Lv |
| R |
稳定时棒处于平衡状态,故有:
F=mgsinθ+B2I′L
由以上各式代入数值,得棒的稳定速度为:v=2m/s.
故选:B
点评:解决本题的关键掌握从线圈处于中性面开始计时,电动势的瞬时表达式e=Emsinωt以及峰值Em=NB1Sω,棒达到稳定速度时,处于平衡状态,根据平衡条件列式求解,难度适中.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 如图所示,匝数为100、边长为0.2m的正方形线圈,在磁感应强度B为2T的匀强磁场中,从中性面开始以10πrad/s的角速度绕OO′轴匀速转动.若线圈自身电阻为2Ω,负载电阻R=6Ω,π2=10,则开始转动0.05s内R上的热量为多少焦耳?
如图所示,匝数为100、边长为0.2m的正方形线圈,在磁感应强度B为2T的匀强磁场中,从中性面开始以10πrad/s的角速度绕OO′轴匀速转动.若线圈自身电阻为2Ω,负载电阻R=6Ω,π2=10,则开始转动0.05s内R上的热量为多少焦耳?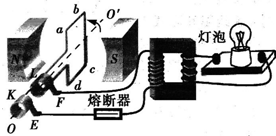 如图所示,匝数为100匝的矩形线圈abcd处于磁感应强度B=
如图所示,匝数为100匝的矩形线圈abcd处于磁感应强度B=
 T的水平匀强磁场中,线圈面积S=0.5m2,内阻不计.线圈绕垂直于磁场的轴以角速度ω=10π rad/s匀速转动。线圈通过金属滑环与理想变压器原线圈相连,变压器的副线圈接入一只“12V,12W”灯泡,灯泡正常发光,下列说法中正确的是
T的水平匀强磁场中,线圈面积S=0.5m2,内阻不计.线圈绕垂直于磁场的轴以角速度ω=10π rad/s匀速转动。线圈通过金属滑环与理想变压器原线圈相连,变压器的副线圈接入一只“12V,12W”灯泡,灯泡正常发光,下列说法中正确的是 s内在电阻R上产生的热量为多少焦耳?
s内在电阻R上产生的热量为多少焦耳? 