��Ŀ����
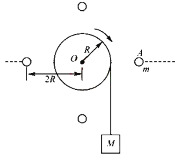
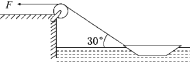
����Ŀ����ͼ��һ����m��2kg��С����ܵ�ƽ��б�������F��22N����A���ɾ�ֹ������б���������ȼ����˶���б���㹻����б���������37�㣨��֪С�����б���Ķ�Ħ����������0.5��gȡ10m/s2��sin37�㣽0.6��cos37�㣽0.8������
��1��С����˶��ļ��ٶ�a
��2����F����4s��ȥ��С����ϻ������о�A��������SA
��3�����ӳ�ȥ��F��ʼ��ʱ��С��龭�ʱ�佫������A���Ϸ�8.35m��B�㡣

���𰸡���1��1m/s2������ƽ����б�����ϣ���2��8.8m����3��0.1s��1.07s��
��������
��ţ�ٵڶ����ɵã�
F��mgsin������mgcos����ma��
��ã�a��1m/s2��
(2)4s������λ�ƣ�
x1��![]() at12��
at12��![]() ��1��42m��8m��
��1��42m��8m��
��ȥ����ʱ�����ٶ���
v��at1��1��4 m/s��4m/s��
��ȥ��������ţ�ٵڶ����ɵã�
mgsin��+��mgcos����ma��
��ã�a����10m/s2��
��ȥ�����������λ�ƣ�
x2��![]() ��
��![]() ��0.8m��
��0.8m��
С����ϻ����̾�A��������룺
SA��x1+x2��8.8m��
�ӳ�ȥ����������B���λ�ƣ�
x��(8.35��8)m��0.35m��
�������ϻ������̵���B��ʱ���ٶȣ�
vB��![]() ��3m/s��
��3m/s��
����B���ʱ�䣺
tB��![]() ��
��![]() s��0.1s��
s��0.1s��
�ӳ�ȥ�����������ٶ�Ϊ����Ҫ��ʱ�䣺
t2��![]() ��
��![]() ��0.4s��
��0.4s��
��鵽����ߵ�������˶����̣����ٶȣ�
a1��![]() ��gsin������gcos����2m/s2��
��gsin������gcos����2m/s2��
������ߵ㷵�ص�B����Ҫ��ʱ�䣺
t3��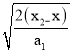 ��
��![]() s��0.67s��
s��0.67s��
����»����̾���B����Ҫ��ʱ�䣺
t��t2+t3��0.4s+0.67s��1.07s��
��(1)С����˶��ļ��ٶ�a��СΪ1m/s2������ƽ����б�����ϣ�
(2)��F����4s��ȥ��С����ϻ������о�A��������SAΪ8.8m��
(3)�ӳ�ȥ��F��ʼ��ʱ��С��龭������A���Ϸ�8.35m��B����Ҫ��ʱ��Ϊ0.1s��1.07s��