题目内容
7. 如图所示,在光滑的水平面上放着两块长度相同、质量分别为M1和M2的木板,两个大小、质量完全相同(可视为质点)的小滑块分别以初速度v01和v02冲上木板,且都能与木板分离,分离时两木板的速度分别为v1和v2,若已知v2>v1,且滑块与木板间的动摩擦因数相同,则以下情况不可能存在的是( )
如图所示,在光滑的水平面上放着两块长度相同、质量分别为M1和M2的木板,两个大小、质量完全相同(可视为质点)的小滑块分别以初速度v01和v02冲上木板,且都能与木板分离,分离时两木板的速度分别为v1和v2,若已知v2>v1,且滑块与木板间的动摩擦因数相同,则以下情况不可能存在的是( )| A. | v01>v02,且M1=M2 | B. | v01=v02,且M1>M2 | C. | v01<v02,且M1<M2 | D. | v01<v02,且M1>M2 |
分析 根据牛顿第二定律比较出物块和木板的加速度大小,结合位移之差等于板长,比较运动的时间,从而结合速度时间公式比较分离时木板的速度大小,逐项分析判断.
解答 解:物块做匀减速直线运动的加速度大小为:a=$\frac{μmg}{m}=μg$,木板做匀加速直线运动的加速度大小为:$a′=\frac{μmg}{M}$,
A、若M1=M2,则木板做匀加速直线运动的加速度大小相等,根据${v}_{0}t-\frac{1}{2}a{t}^{2}-\frac{1}{2}a′{t}^{2}=L$知,因为物块和木板的加速度都相同,初速度大的运动的时间较短,根据v=at知,v2>v1,故A可能存在.
B、若M1>M2,则木板的加速度a1′<a2′,根据${v}_{0}t-\frac{1}{2}a{t}^{2}-\frac{1}{2}a′{t}^{2}=L$知,初速度相同,木板加速度小的运动时间较短,即t2>t1,根据速度时间公式得,v2>v1,故B可能存在.
C、若M1<M2,则木板的加速度a1′>a2′,根据${v}_{0}t-\frac{1}{2}a{t}^{2}-\frac{1}{2}a′{t}^{2}=L$知,物块1的初速度小,上面木板的加速度大,则上面物块滑离的时间长,根据速度时间公式知,v2<v1,故C不可能存在.
D、若M1>M2,则木板的加速度a1′<a2′,根据${v}_{0}t-\frac{1}{2}a{t}^{2}-\frac{1}{2}a′{t}^{2}=L$知,物块1的初速度小,上面木板的加速度小,则上面物块滑离的时间可能短,则下面物块滑离的时间可能长,根据速度时间公式知,v2可能大于v1,故D可能存在.
本题选不可能存在的,故选:C.
点评 解决本题的关键正确地受力分析,结合牛顿第二定律和运动学公式,抓住物块的位移和木板的位移之差等于板长分析求解.

| A. |  | B. |  | C. |  | D. |  |
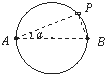 水平面内有一光滑绝缘细圆环,在它某一直径的两个端点A和B固定电荷量分别为Q1、Q2的正点电荷,圆环上穿着一个带电小球q(可视为点电荷)可沿环自由滑动,如图所示.如果要使小球在P点恰能保持静止,那么PA与AB的夹角?与Q1、Q2的关系应满足( )
水平面内有一光滑绝缘细圆环,在它某一直径的两个端点A和B固定电荷量分别为Q1、Q2的正点电荷,圆环上穿着一个带电小球q(可视为点电荷)可沿环自由滑动,如图所示.如果要使小球在P点恰能保持静止,那么PA与AB的夹角?与Q1、Q2的关系应满足( )| A. | tan3α=$\frac{{Q}_{2}}{{Q}_{1}}$ | B. | tan2α=$\frac{{Q}_{2}}{{Q}_{1}}$ | C. | tan2α=$\frac{{Q}_{1}}{{Q}_{2}}$ | D. | tanα=$\frac{{Q}_{1}}{{Q}_{2}}$ |
 在竖直平面内,有一根光滑金属杆弯成如图所示形状,相应的曲线方程为y=Acosx,将一个小环套在该金属杆上,并从x=0、y=A处以某一初速度沿路径ABCDE 运动.则在运动过程中( )
在竖直平面内,有一根光滑金属杆弯成如图所示形状,相应的曲线方程为y=Acosx,将一个小环套在该金属杆上,并从x=0、y=A处以某一初速度沿路径ABCDE 运动.则在运动过程中( )| A. | 小环在B点的速度最大 | B. | 小环在C点的速度最大 | ||
| C. | 小环在B点和D点的加速度大小相同 | D. | 小环在C点和E点的加速度大小相同 |
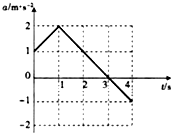 某同学在开展研究性学习的过程中,利用加速度传感器研究某一物体以初速度2m/s做直线运动的加速度a随时间t变化的规律,并在计算机上得到了前4s内物体加速度随时间变化的关系图象,如图所示.以物体的初速度方向为正方向,则下列说法正确的是( )
某同学在开展研究性学习的过程中,利用加速度传感器研究某一物体以初速度2m/s做直线运动的加速度a随时间t变化的规律,并在计算机上得到了前4s内物体加速度随时间变化的关系图象,如图所示.以物体的初速度方向为正方向,则下列说法正确的是( )| A. | 物体在1s末加速度方向改变 | |
| B. | 物体在3s末速度方向改变 | |
| C. | 前4s内物体的最大速度出现在第1s末 | |
| D. | 物体在第2s末与第4s末的速度相同 |
 如图所示,一圆盘可绕通过圆盘中心且垂直于盘面的竖直轴转动,在圆盘上放置一小木块,它随圆盘一起做匀速圆周运动.关于小木块的受力,下列说法正确的是( )
如图所示,一圆盘可绕通过圆盘中心且垂直于盘面的竖直轴转动,在圆盘上放置一小木块,它随圆盘一起做匀速圆周运动.关于小木块的受力,下列说法正确的是( )| A. | 木块受重力和压力 | |
| B. | 木块受重力和支持力 | |
| C. | 木块受重力、支持力和摩擦力 | |
| D. | 木块受重力、支持力、摩擦力和向心力 |
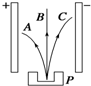 贝可勒尔发现天然放射现象,揭开了人类研究原子核结构的序幕.如图7中P为放在匀强电场中的天然放射源,其放出的射线在电场中分成A、B、C三束.
贝可勒尔发现天然放射现象,揭开了人类研究原子核结构的序幕.如图7中P为放在匀强电场中的天然放射源,其放出的射线在电场中分成A、B、C三束. 在光滑的冰面上放置一个截面圆弧为四分之一圆的半径足够大的光滑自由曲面体,一个坐在冰车上的小孩手扶一小球静止在冰面上.已知小孩和冰车的总质量为m1小球的质量为m2,曲面体的质量为m3.某时刻小孩将小球以v0=4m/s的速度向曲面体推出(如图所示).
在光滑的冰面上放置一个截面圆弧为四分之一圆的半径足够大的光滑自由曲面体,一个坐在冰车上的小孩手扶一小球静止在冰面上.已知小孩和冰车的总质量为m1小球的质量为m2,曲面体的质量为m3.某时刻小孩将小球以v0=4m/s的速度向曲面体推出(如图所示).