题目内容
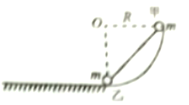
【题目】如图所示,半径为R=0.4m的![]() 圆弧形光滑轨道固定于竖直平面内,圆弧形轨道与光滑固定的水平轨道相切,可视为质点的质量均为m=0.5kg的小球甲、乙用轻杆连接,置于圆弧形轨道上,小球甲与O点等高,小球乙位于圆心O的正下方.某时刻将两小球山静止释放,最终它们在平面上运动,g取10m/s2,则
圆弧形光滑轨道固定于竖直平面内,圆弧形轨道与光滑固定的水平轨道相切,可视为质点的质量均为m=0.5kg的小球甲、乙用轻杆连接,置于圆弧形轨道上,小球甲与O点等高,小球乙位于圆心O的正下方.某时刻将两小球山静止释放,最终它们在平面上运动,g取10m/s2,则
A.两小球由静止释放后速度大小相等,最终在水平面上运动的速度大小为2m/s
B.小球甲下滑过程中重力对它做功的功率一直增大
C.小球甲下滑到圆弧轨道最低点对轨道的压力的大小为10N
D.整个过程中轻杆对小球乙做的功为为1J
【答案】CD
【解析】
A.两球沿杆方向速度始终大小一样,但在甲球未滑离圆弧形轨道时,两球实际速度不相等;当甲乙两球都在水平面上运动时,两球速度相等.整个过程两个小球组成系统机械能守恒,故:
![]()
解得小球在水平面上最终运动速度
![]() =2m/s
=2m/s
故A错误;
B.小球甲下滑过程中,最高点速度为零,故重力的功率为零;最低点速度和重力垂直,故重力的功率也是零;而中途重力的功率不为零,故重力的功率应该是先增加后减小,故B错误;
C.小球甲下滑到圆弧形轨道最低点,重力和支持力的合力提供向心力,故:
![]()
解得:
N=10N
根据牛顿第三定律,压力也为10N,故C正确;
D.整个过程中,对球乙,根据动能定理,有:
![]() =-1J
=-1J
故D正确.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目