题目内容
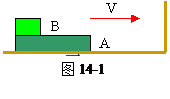
如图所示,被压缩后锁定的弹簧一端固定在墙上,另一端与质量为2m的物体A相连接,光滑的水平面和光滑的曲面平滑相连.有一质量为m的物体B,从高h处由静止开始沿光滑曲面滑下,与物体A相碰,碰后两物体立即以相同速度向右运动(但两个物体不粘连),同时弹簧的锁定被解除,返回时物体B能上升的最大高度为
h,试求:
(1)碰撞结束瞬间A、B的共同速度v1.
(2)弹簧锁定时对应的弹性势能Ep.

| 1 |
| 2 |
(1)碰撞结束瞬间A、B的共同速度v1.
(2)弹簧锁定时对应的弹性势能Ep.

(1)设B从高h处滑到平面时的速度为v0,由动能定理有
mgh=
m
-0,解得v0=
.
设A与B碰后的共同速度为v1,根据动量守恒定律有mv0=(m+2m)v1,
可得v1=
.
(2)设B返回时离开A的速度为v′0,则
mg
h=
mv
解得 v′0=
=
对A、B和弹簧有
?3m
+Ep=
?3mv
,
得Ep=
mgh
答:
(1)碰撞结束瞬间A、B的共同速度v1是
.
(2)弹簧锁定时对应的弹性势能Ep是
mgh.
mgh=
| 1 |
| 2 |
| v | 20 |
| 2gh |
设A与B碰后的共同速度为v1,根据动量守恒定律有mv0=(m+2m)v1,
可得v1=
| ||
| 3 |
(2)设B返回时离开A的速度为v′0,则
mg
| 1 |
| 2 |
| 1 |
| 2 |
| ′ | 20 |
解得 v′0=
2g
|
| gh |
对A、B和弹簧有
| 1 |
| 2 |
| v | 21 |
| 1 |
| 2 |
| ′ | 20 |
得Ep=
| 7 |
| 6 |
答:
(1)碰撞结束瞬间A、B的共同速度v1是
| ||
| 3 |
(2)弹簧锁定时对应的弹性势能Ep是
| 7 |
| 6 |

练习册系列答案
相关题目