题目内容
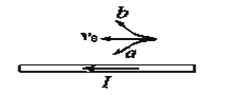
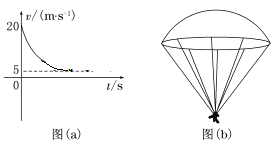
【题目】某运动员做跳伞训练,他从悬停在空中的直升机上由静止跳下,跳离直升机一段时间后打开降落伞减速下落,他打开降落伞后的速度-时间图象如图(a)所示。降落伞用8根对称的悬绳悬挂运动员,每根悬绳与中轴线的夹角为37°,如图(b)所示。已知运动员和降落伞的质量均为50 kg,不计运动员所受的阻力,打开降落伞后,降落伞所受的阻力f与下落速度v成正比,即f=kv。重力加速度g取10 m/s2,sin 37°=0.6,cos 37°=0.8。求:
(1)打开降落伞前运动员下落的高度;
(2)阻力系数k和打开降落伞瞬间的加速度;
(3)降落伞的悬绳能够承受的拉力至少为多少。
【答案】(1)20m(2)30 m/s2,方向竖直向上。(3)312.5 N
【解析】
(1)根据速度位移公式求出打开降落伞前人下落的高度。
(2)抓住平衡,根据kv=(m1+m2)g求出阻力系数,根据牛顿第二定律求出加速度的大小。
(3)对人分析,根据牛顿第二定律求出拉力的大小。
(1)打开降落伞前运动员做自由落体运动,根据速度位移公式可得运动员下落的高度为:h=![]() ,
,
由题图(a)可知:v0=20m/s
解得:h=20m。
(2)由题图(a)可知,当速度为v=5m/s时,运动员做匀速运动,受力达到平衡状态,
由平衡条件可得:kv=2mg
即![]() ,
,
解得:k=200Ns/m。
在打开降落伞瞬间,由牛顿第二定律可得:kv0-2mg=2ma,
解得:a=30m/s2,方向竖直向上。
(3)根据题意可知,打开降落伞瞬间悬绳对运动员拉力最大,设此时降落伞上每根悬绳的拉力为T,以运动员为研究对象,则有:8Tcos37°-mg=ma,
代入数据可解得:T=312.5N,
故悬绳能够承受的拉力至少为312.5N。

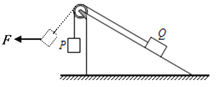
【题目】现用频闪照相方法来研究物块的变速运动.在一小物块沿斜面向下运动的过程中,用频闪相机拍摄的不同时刻物块的位置如图所示.拍摄时频闪频率是10 Hz,通过斜面上固定的刻度尺读取的5个连续影像间的距离依次为x1、x2、x3、x4.已知斜面顶端的高度h和斜面的长度s.数据如下表所示.重力加速度大小g=9.80 m/s2.
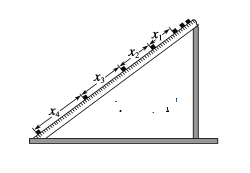
单位:cm
x1 | x2 | x3 | x4 | h | s |
10.76 | 15.05 | 19.34 | 23.65 | 48.00 | 80.00 |
根据表中数据,完成下列填空:
(1)物块的加速度a=________ m/s2(保留3位有效数字)
(2)因为________,可知斜面是粗糙的.