题目内容
5. 一长为L=0.2m的圆管竖直放置,顶端固定一个弹性小球,管的下端离地面距离为H=0.6m,释放小球让其自由落下,当球运动到管口时,释放圆管,球落地后被竖直向上弹起,反弹的速度大小与落地时的速度大小相等.不计空气阻力,不计球与地面碰撞所用的时间,重力加速度为g=10m/s2.求:
一长为L=0.2m的圆管竖直放置,顶端固定一个弹性小球,管的下端离地面距离为H=0.6m,释放小球让其自由落下,当球运动到管口时,释放圆管,球落地后被竖直向上弹起,反弹的速度大小与落地时的速度大小相等.不计空气阻力,不计球与地面碰撞所用的时间,重力加速度为g=10m/s2.求:(1)球落地时的速度大小;
(2)球落地时管的下端离地面的距离及管的速度大小;
(3)球反弹后再次回到管的顶端所用的时间.
分析 (1)小球做自由落体运动,根据速度位移公式求的即可
(2)根据位移时间公式求的时间,由h=$\frac{1}{2}g{t}^{2}$即v=gt即可求得
(3)由位移时间公式即可求得时间
解答 解:(1)根据速度位移公式可得2g(L+H)=v2
解得v=$\sqrt{2g(L+H)}$=4m/s
(2)球下落L所需时间为t1,L=$\frac{1}{2}{gt}_{1}^{2}$,解得${t}_{1}=\sqrt{\frac{2L}{g}}$=0.2s
球下落L+H所需时间为t2,$H+L=\frac{1}{2}{gt}_{2}^{2}$,解得${t}_{2}=\sqrt{\frac{2(H+L)}{g}}$=0.4s
球落地时管下降的高度为$h=\frac{1}{2}g({t}_{2}-{t}_{1})^{2}$=0.2m
距地面的高度为△h=H-h=0.4m
管的速度为v=g(t2-t1)=2m/s
(3)球反弹后的速度为v=4m/s
设经历时间t回到管的顶端
${h}_{1}=v′t+\frac{1}{2}g{t}^{2}$
${h}_{2}=vt-\frac{1}{2}g{t}^{2}$
△h=h1+h2
联立解得$t=\frac{1}{15}s$
答:(1)球落地时的速度大小为4m/s;
(2)球落地时管的下端离地面的距离及管的速度大小分别为0.4m,2m/s;
(3)球反弹后再次回到管的顶端所用的时间为$\frac{1}{15}s$.
点评 本题的难点在于管和球的运动情况难于判断,关键通过计算理清球和管的运动规律,利用好运动学公式进行求解

练习册系列答案
相关题目
13.一物体自t=0时开始做直线运动,其速度图线如图所示.下列选项正确的是( )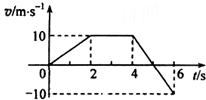

| A. | 在0~6s内,物体离出发点最远为35m | |
| B. | 在0~6s内,物体经过的路程为35m | |
| C. | 在1s时和4.5秒时物体加速度方向相同 | |
| D. | 在1s时和4.5秒时物体速度方向相同 |
10.做匀加速沿直线运动的质点在第一个3s内的平均速度比它在第一个5s内的平均速度小3m/s,质点质量为1kg,则质点受到的合外力大小为( )
| A. | 1N | B. | 2N | C. | 3 N | D. | 4 N |
 如图所示.带箭头的曲线表示一个带负电的粒子通过-个点电荷Q所产生的电场的运动轨迹,虚线表示点电荷电场的两个等势面,则比较A、B两点的电势大小和场强大小有:φA>φB,EA<EB,比较带负电离子在A、B两点的速度和加速度大小有:vA>vB,aA<aB.
如图所示.带箭头的曲线表示一个带负电的粒子通过-个点电荷Q所产生的电场的运动轨迹,虚线表示点电荷电场的两个等势面,则比较A、B两点的电势大小和场强大小有:φA>φB,EA<EB,比较带负电离子在A、B两点的速度和加速度大小有:vA>vB,aA<aB. 如图所示,有一质量为M=2kg 的平板小车静止在光滑的水平地面上,现有质量均为m=1kg 的小物块A和B(均可视为质点),由车上P处开始,A以初速度v1=2m/s向左运动,B同时以v2=4m/s 向右运动.最终A、B两物块恰好停在小车两端没有脱离小车.两物块与小车间的动摩擦因数都为μ=0.1,取g=10m/s2.求:
如图所示,有一质量为M=2kg 的平板小车静止在光滑的水平地面上,现有质量均为m=1kg 的小物块A和B(均可视为质点),由车上P处开始,A以初速度v1=2m/s向左运动,B同时以v2=4m/s 向右运动.最终A、B两物块恰好停在小车两端没有脱离小车.两物块与小车间的动摩擦因数都为μ=0.1,取g=10m/s2.求: 如图所示为一质量为1Kg的小球做平抛运动的闪光照相照片的一部分,图中背景方格的边长均为10cm.如果取g=10m/s2,那么:
如图所示为一质量为1Kg的小球做平抛运动的闪光照相照片的一部分,图中背景方格的边长均为10cm.如果取g=10m/s2,那么: