题目内容
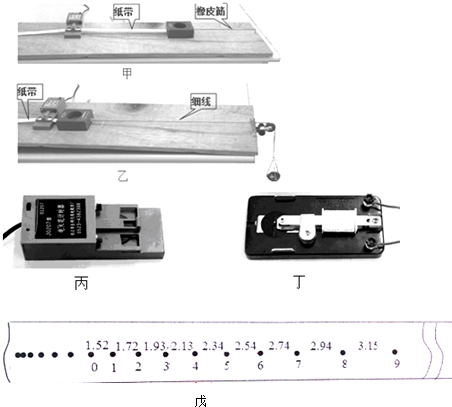
12. 如图所示,固定在水平地面上的光滑长直导轨槽,(图为俯视图,图中两组平行双直线表示槽的两侧壁).槽内放置一个滑块,滑块的左半部是半径为R的半圆柱形光滑凹槽,滑块的宽度为2R,恰与槽的两内侧壁的间距相等,滑块可在槽内沿槽壁自由滑动.现有一金属小球(可视为质点)以水平初速度v0沿槽的一侧壁冲向滑块,从滑块的半圆形槽口边缘进入滑块凹槽.已知金属小球的质量为m,滑块的质量为3m,整个运动过程中无机械能损失.求:
如图所示,固定在水平地面上的光滑长直导轨槽,(图为俯视图,图中两组平行双直线表示槽的两侧壁).槽内放置一个滑块,滑块的左半部是半径为R的半圆柱形光滑凹槽,滑块的宽度为2R,恰与槽的两内侧壁的间距相等,滑块可在槽内沿槽壁自由滑动.现有一金属小球(可视为质点)以水平初速度v0沿槽的一侧壁冲向滑块,从滑块的半圆形槽口边缘进入滑块凹槽.已知金属小球的质量为m,滑块的质量为3m,整个运动过程中无机械能损失.求:(1)当金属小球滑离滑块时,金属小球和滑块的速度各是多大;
(2)当金属小球经过滑块上的半圆柱形槽的最右端A点时,金属小球的对地速率.
分析 (1)小球与滑块作用的过程中,系统的动量守恒,机械能守恒,根据两大守恒求解金属小球滑离木质滑块时两者的速度大小;
(2)小球过A点时沿轨道方向两者有共同速度,根据动量守恒求出共同速度,根据机械能守恒求解金属小球的对地速率.
解答 解:(1)设滑离时小球和滑块的速度分别为v1和v2,球与滑块组成的系统动量守恒,以向右为正方向,由动量守恒定律得:
mv0=mv1+3mv2,
在整个运动过程中无机械能损失,由机械能守恒定律得:
$\frac{1}{2}$mv02=$\frac{1}{2}$mv12+$\frac{1}{2}$•3mv22,
解得:v1=-$\frac{{v}_{0}}{2}$,负号表示方向向左,v2=$\frac{{v}_{0}}{2}$;
(2)小球过A点时沿轨道方向两者有共同速度v,设小球对地速度为v′,以向右为正方向,由轨道方向动量守恒得:
mv0=(m+3m)v,
由机械能守恒定律得:$\frac{1}{2}$mv02=$\frac{1}{2}$•3mv2+$\frac{1}{2}$mv′2,
解得:v=$\frac{{v}_{0}}{4}$,v′=$\frac{\sqrt{13}}{4}$v0;
答:(1)当金属小球滑离滑块时,金属小球和滑块的速度分别为$\frac{{v}_{0}}{2}$,方向:向左,v2=$\frac{{v}_{0}}{2}$,方向:水平向右;
(2)当金属小球经过滑块上的半圆柱形槽的最右端A点时,金属小球的对地速率$\frac{\sqrt{13}}{4}$v0.
点评 本题考查了求速度问题,解答此题的关键在于整个过程中满足机械能守恒和动量守恒,难点是抓住小球过A点时沿轨道方向两者有共同速度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
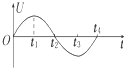
2.LC回路中电容器两端电压U随时间t变化的关系如图所示,则( )

| A. | 在时刻t2,电路中的电流为零 | |
| B. | 在时刻t3,电路中的磁场能最大 | |
| C. | 从时刻t2至t3,电路中的电场能不断增大 | |
| D. | 从时刻t3至t4,电容器所带的电荷量不断增大 |
3.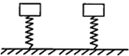 如图所示,两根完全相同的轻质弹簧,下端固定在地面上,质量不同、形状相同的两物块分别置于两弹簧上端但不栓接,现用外力作用在物体上,使两弹簧具有相同的压缩量,撤去外力后,两物块由静止向上运动并离开弹簧,则从撤去外力到物块速度第一次减为零的过程,两物块一定满足(弹簧始终在弹性限度之内,以地面为零势能面)( )
如图所示,两根完全相同的轻质弹簧,下端固定在地面上,质量不同、形状相同的两物块分别置于两弹簧上端但不栓接,现用外力作用在物体上,使两弹簧具有相同的压缩量,撤去外力后,两物块由静止向上运动并离开弹簧,则从撤去外力到物块速度第一次减为零的过程,两物块一定满足(弹簧始终在弹性限度之内,以地面为零势能面)( )
 如图所示,两根完全相同的轻质弹簧,下端固定在地面上,质量不同、形状相同的两物块分别置于两弹簧上端但不栓接,现用外力作用在物体上,使两弹簧具有相同的压缩量,撤去外力后,两物块由静止向上运动并离开弹簧,则从撤去外力到物块速度第一次减为零的过程,两物块一定满足(弹簧始终在弹性限度之内,以地面为零势能面)( )
如图所示,两根完全相同的轻质弹簧,下端固定在地面上,质量不同、形状相同的两物块分别置于两弹簧上端但不栓接,现用外力作用在物体上,使两弹簧具有相同的压缩量,撤去外力后,两物块由静止向上运动并离开弹簧,则从撤去外力到物块速度第一次减为零的过程,两物块一定满足(弹簧始终在弹性限度之内,以地面为零势能面)( )| A. | 两物块达最大速度时的高度相同 | B. | 上升的最大高度不同 | ||
| C. | 最大加速度相同 | D. | 最大重力势能不同 |
20.如图所示,两束单色光a,b射向水面A点,经折射后组成一束复色光,则( )

| A. | 在水中a光的速度比b光的速度小 | |
| B. | 以水下S点为光源向水面发射复色光,a光更容易发生全反射 | |
| C. | 用同一双缝干涉实验装置做实验,a光的干涉条纹间距大于b光的间距 | |
| D. | 若a、b两束光的入射角均增加相同角度,经水的折射后仍能组成一束复色光 |
7.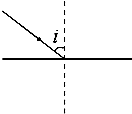 如图所示,一束光从空气中射向临界角为45°的某种玻璃的表面,i表示入射角,则下列说法中不正确的是( )
如图所示,一束光从空气中射向临界角为45°的某种玻璃的表面,i表示入射角,则下列说法中不正确的是( )
 如图所示,一束光从空气中射向临界角为45°的某种玻璃的表面,i表示入射角,则下列说法中不正确的是( )
如图所示,一束光从空气中射向临界角为45°的某种玻璃的表面,i表示入射角,则下列说法中不正确的是( )| A. | 当i>45°时会发生全反射现象 | |
| B. | 无论入射角多大,折射角r都不会超过45° | |
| C. | 欲使折射角为30°,应以i=45°的角度入射 | |
| D. | 此光在该玻璃中的速度为$\frac{{\sqrt{2}}}{2}$c(c为光束在真空中的速度) |
17.宇航员在月球表面以初速度v0将一石块与水平方向成θ角斜向上抛出,小球上升的最大高度为h,月球的半径为R,引力常量为G.由此可推算( )
| A. | 月球表面的重力加速度为$\frac{{{v}_{0}}^{2}co{s}^{2}θ}{2h}$ | |
| B. | 月球的质量为$\frac{{{v}_{0}}^{2}{R}^{2}si{n}^{2}θ}{2Gh}$ | |
| C. | 石块在空中的运动时间为$\frac{2h}{{v}_{0}sinθ}$ | |
| D. | 月球的第一宇宙速度为v0sinθ$\sqrt{\frac{R}{h}}$ |
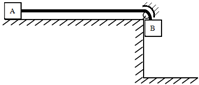 如图,A、B两物体通过一柔软且不可伸长的绳子连接,跨在光滑小滑轮两侧,软绳与水平接触面平行,已知A、B两物体的质量均为m,且可视为质点,软绳质量也为m,长为2L,平台离地高L,不计运动过程中的一切摩擦,刚开始软绳全部在水平面内,现无初速释放B,A、B在重力作用下开始运动,若B触地后不再反弹.求:
如图,A、B两物体通过一柔软且不可伸长的绳子连接,跨在光滑小滑轮两侧,软绳与水平接触面平行,已知A、B两物体的质量均为m,且可视为质点,软绳质量也为m,长为2L,平台离地高L,不计运动过程中的一切摩擦,刚开始软绳全部在水平面内,现无初速释放B,A、B在重力作用下开始运动,若B触地后不再反弹.求: