��Ŀ����
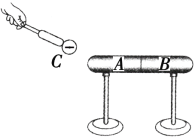
����Ŀ����ͼ��ʾ��һ�㹻����ˮƽ���ʹ����ٶ�v= 2m/s�����˶�������Ϊm1 = 1kg��С���P������Ϊm2 = 1.5kg��С���Q��ͨ�������ֵ��������ӣ������㹻���Ҳ����쳤��ijʱ�����P�Ӵ��ʹ�������ٶ�v0 = 4m/s���ϴ��ʹ���P�붨���ּ������ˮƽ����֪���P�봫�ʹ���Ķ�Ħ��������= 0.5���������ٶ�Ϊg =10m/s2�����ƻ��ֵ�������Ħ���������˶����������Q��û�������������ִ�����

(1)���P�ճ��ϴ��ʹ�ʱ�ļ��ٶȴ�С��
(2)���P�ճ��ϴ��ʹ����ҷ���Զ���Ĺ����У�PQϵͳ��е�ܵĸı�����
(3)�����ʹ��Բ�ͬ���ٶ�v��0 <v<v0�������˶�����vȡ���ʱ���P���ҳ嵽��Զ��ʱ��P�봫�ʹ��������Ħ��������С������СֵΪ���
���𰸡�(1)a1=8m/s2 (2) ![]() (3)
(3) ![]() ,
, ![]()
�������������������1�����P�ճ��ϴ��ʹ�ʱ��P�ij��ٶȴ��ڴ��ʹ����ٶȣ���P��Դ��ʹ������˶�����P�ܵ������Ħ�������ã��ֱ��P��Q������������ţ�ٵڶ�������ʽ�����ٶȣ���2����P�봫�ʹ����ٺ���Ħ����![]() ������P�����������˶���PQϵͳ��е�ܵĸı�������Ħ������P���Ĺ�����3�������μ����˶������λ�ƣ���������
������P�����������˶���PQϵͳ��е�ܵĸı�������Ħ������P���Ĺ�����3�������μ����˶������λ�ƣ���������![]() ��ʽ�������.
��ʽ�������.
��1�����P�ճ��ϴ��ʹ�ʱ����PQ�ļ��ٶ�Ϊ![]() ������������Ϊ
������������Ϊ![]()
��P�ij��ٶȴ��ڴ��ʹ����ٶȣ���P��Դ��ʹ������˶�����P�ܵ������Ħ��������
��P��ţ�ٵڶ����ɵã� ![]()
��Q����������֪������ֱ���������µ����������ϵ���������
��ţ�ٵڶ����ɵã� ![]()
������ã� ![]()
��2��P�ȼ��ٵ��봫�ʹ��ٶ���ͬ����λ��Ϊ![]() ����
����![]()
���ٺ�����Ħ����![]()
��P�������洫�ʹ�һ�������˶����������Ҽ��٣�Ħ��������ˮƽ����
���ʱ�ļ��ٶ�Ϊ![]() ������������Ϊ
������������Ϊ![]()
��P��ţ�ٵڶ����ɵã� ![]()
��Q��ţ�ٵڶ����ɵã� ![]()
������ã� ![]()
����ٵ�0λ��Ϊ![]() ����
����![]()
PQϵͳ��е�ܵĸı�������Ħ������P���Ĺ��� ![]()
��3����һ�����ٹ��̣�����ʱ��![]() ��P�˶���λ��Ϊ
��P�˶���λ��Ϊ![]() ��Ƥ���˶���λ��Ϊ
��Ƥ���˶���λ��Ϊ![]()
�ڶ������ٹ���������ʱ��![]() ��P�˶���λ��Ϊ
��P�˶���λ��Ϊ![]() ��Ƥ���˶���λ��Ϊ
��Ƥ���˶���λ��Ϊ![]()
���������̲���������![]()
��![]() ʱ��
ʱ�� ![]()

 ����ͼ���������������ϵ�д�
����ͼ���������������ϵ�д� ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д�