题目内容
14.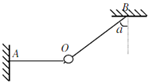 如图所示,小球用轻质橡皮条AO与不可伸长的细线BO悬吊着,且AO呈水平状态,BO跟竖直方向的夹角为α,那么在剪断AO或BO的瞬间,小球的加速度情况是( )
如图所示,小球用轻质橡皮条AO与不可伸长的细线BO悬吊着,且AO呈水平状态,BO跟竖直方向的夹角为α,那么在剪断AO或BO的瞬间,小球的加速度情况是( )| A. | 剪断AO瞬间,小球加速度大小a=gtanα | |
| B. | 前断AO瞬间,小球加速度大小a=gsinα | |
| C. | 剪断BO瞬间,小球加速度大小a=$\frac{g}{cosα}$ | |
| D. | 不管剪断哪一根,小球加速度均是零 |
分析 先根据平衡条件求出剪断橡皮条前两根橡皮条的拉力大小,在剪断某一根橡皮条的瞬间,另一根橡皮条拉力大小不变,再根据牛顿第二定律求解瞬间的加速度大小.
解答 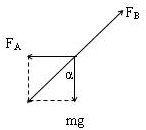 解:以小球为研究对象,剪断橡皮条前其受力情况如图,根据平衡条件,
解:以小球为研究对象,剪断橡皮条前其受力情况如图,根据平衡条件,
AO绳的拉力大小为FA=mgtanα,BO绳的拉力大小为FB=$\frac{mg}{cosα}$
若剪断AO瞬间,FA=0,FB突变,则此瞬间小球所受的合力大小等于FA=mgsinα,所以加速度大小为a=gsinα.
剪断BO瞬间,FB=0,FA不变,则此瞬间小球所受的合力大小等于FB=$\frac{mg}{cosα}$,方向与原来FB相反,所以加速度大小为a=$\frac{g}{cosα}$.
故选:BC
点评 本题是瞬时问题,先分析橡皮条剪断前小球的受力情况,再分析剪断橡皮条瞬间小球的受力情况,抓住橡皮条与弹簧类似的特性:弹力不能突变,根据牛顿第二定律求解瞬间的加速度.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
7. 如图所示,折线是表示物体甲从A地向B地运动的位移图象,直线表示物体乙从B地向A地运动的位移图象,则下列说法正确的是( )
如图所示,折线是表示物体甲从A地向B地运动的位移图象,直线表示物体乙从B地向A地运动的位移图象,则下列说法正确的是( )
 如图所示,折线是表示物体甲从A地向B地运动的位移图象,直线表示物体乙从B地向A地运动的位移图象,则下列说法正确的是( )
如图所示,折线是表示物体甲从A地向B地运动的位移图象,直线表示物体乙从B地向A地运动的位移图象,则下列说法正确的是( )| A. | 甲、乙两物体都做匀速运动 | |
| B. | 乙做匀速运动,速度大小为12.5m/s | |
| C. | 甲、乙两物体运动8s后,在距甲的出发点60m处相遇 | |
| D. | 甲在运动过程中停了40s |
2.用比值定义法定义物理量是一种常用的方法,以下四个物理量都是利用比值定义的,其中不是定义式的是( )
| A. | 电场强度E=$\frac{kQ}{{r}^{2}}$ | B. | 加速度a=$\frac{△v}{△t}$ | C. | 电流强度I=$\frac{q}{t}$ | D. | 电容C=$\frac{?S}{4πkd}$ |
9.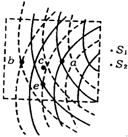 两列简谐横波,波源的振动频率相同,如图为某时刻两列波在介质中相遇的情景,实线表示波峰,虚线表示波谷,则下面说法正确的是( )
两列简谐横波,波源的振动频率相同,如图为某时刻两列波在介质中相遇的情景,实线表示波峰,虚线表示波谷,则下面说法正确的是( )
 两列简谐横波,波源的振动频率相同,如图为某时刻两列波在介质中相遇的情景,实线表示波峰,虚线表示波谷,则下面说法正确的是( )
两列简谐横波,波源的振动频率相同,如图为某时刻两列波在介质中相遇的情景,实线表示波峰,虚线表示波谷,则下面说法正确的是( )| A. | a、b点是干涉加强的位置,c点振动最弱 | |
| B. | 当振源的振动频率同时增加时,干涉区域的干涉图样不发生任何变化 | |
| C. | 再过$\frac{T}{4}$,a、b将变成振动减弱的位置,e点的振动将加强 | |
| D. | a、b、c点是干涉加强的位置,e点振动最弱 |
19.下列叙述中,正确的是( )
| A. | 牛顿发现了万有引力定律,卡文迪许用实验方法测出万有引力恒量的数值,从而使万有引力定律有了真正的实用价值 | |
| B. | 物体做圆周运动,所受的合力一定指向圆心 | |
| C. | 平抛运动是匀变速曲线运动 | |
| D. | 火车超过限定速度转弯时,车轮轮缘将挤压铁轨的内轨 |
6.当斜面倾角为α时,斜面上的物体恰好从斜面匀速下滑,则该物体与斜面之间的摩擦因数μ是( )
| A. | sinα | B. | cosα | C. | tanα | D. | cotα |
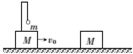 如图所示,光滑水平地面上,在质量M=1kg的滑块上用轻杆及轻绳悬吊质量m=0.5kg的小球.此装置以速度v0=2m/s向右滑动.另一质量也为M的滑块静止于上述装置的右侧.当两滑块相撞后,便粘在一起向右运动,求
如图所示,光滑水平地面上,在质量M=1kg的滑块上用轻杆及轻绳悬吊质量m=0.5kg的小球.此装置以速度v0=2m/s向右滑动.另一质量也为M的滑块静止于上述装置的右侧.当两滑块相撞后,便粘在一起向右运动,求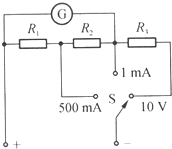 如图是一个电压、电流两用表中的两个电流挡,量程为I1=1mA,I2=500mA;一个电压挡,量程为U=10V.已知表头G的满偏电流Ig=500μA,内阻Rg=600Ω,求电阻R1、R2和R3的阻值.(提示:结果为准备值,列出式子得式子分)
如图是一个电压、电流两用表中的两个电流挡,量程为I1=1mA,I2=500mA;一个电压挡,量程为U=10V.已知表头G的满偏电流Ig=500μA,内阻Rg=600Ω,求电阻R1、R2和R3的阻值.(提示:结果为准备值,列出式子得式子分) 如图所示,一平直的传送带以速率v=4m/s匀速运行,把一工件从A处运送到B处,A、B相距d=12m,工件与传送带间的动摩擦因数μ=0.2.若从A处把工件轻轻放到传送带上,g取10m/s2,那么:
如图所示,一平直的传送带以速率v=4m/s匀速运行,把一工件从A处运送到B处,A、B相距d=12m,工件与传送带间的动摩擦因数μ=0.2.若从A处把工件轻轻放到传送带上,g取10m/s2,那么: