题目内容
4. 如图所示,一平直的传送带以速率v=4m/s匀速运行,把一工件从A处运送到B处,A、B相距d=12m,工件与传送带间的动摩擦因数μ=0.2.若从A处把工件轻轻放到传送带上,g取10m/s2,那么:
如图所示,一平直的传送带以速率v=4m/s匀速运行,把一工件从A处运送到B处,A、B相距d=12m,工件与传送带间的动摩擦因数μ=0.2.若从A处把工件轻轻放到传送带上,g取10m/s2,那么:(1)工件刚开始加速时的加速度多大?
(2)工件经过多长时间能被传送到B处?
分析 (1)根据牛顿第二定律求出工件刚开始加速时的加速度.
(2)根据速度位移公式求出匀加速运动的位移,根据速度时间公式求出匀加速运动的时间,结合匀速运动的位移求出匀速运动的时间,从而得出工件运动的总时间.
解答 解:(1)根据牛顿第二定律得,工件刚开始加速时的加速度a=$\frac{μmg}{m}=μg=0.2×10m/{s}^{2}=2m/{s}^{2}$.
(2)工件匀加速运动的位移${x}_{1}=\frac{{v}^{2}}{2a}=\frac{16}{4}m=4m$,
匀速运动的时间${t}_{2}=\frac{d-{x}_{1}}{v}=\frac{12-4}{4}s=2s$,
匀加速运动的时间${t}_{1}=\frac{v}{a}=\frac{4}{2}s=2s$,
则工件运动的时间t=t1+t2=2+2s=4s.
答:(1)工件刚开始加速时的加速度为2m/s2;
(2)工件经过4s时间能被传送到B处.
点评 解决本题的关键理清工件在整个过程中的运动规律,结合运动学公式灵活求解,难度不大.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
14.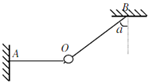 如图所示,小球用轻质橡皮条AO与不可伸长的细线BO悬吊着,且AO呈水平状态,BO跟竖直方向的夹角为α,那么在剪断AO或BO的瞬间,小球的加速度情况是( )
如图所示,小球用轻质橡皮条AO与不可伸长的细线BO悬吊着,且AO呈水平状态,BO跟竖直方向的夹角为α,那么在剪断AO或BO的瞬间,小球的加速度情况是( )
 如图所示,小球用轻质橡皮条AO与不可伸长的细线BO悬吊着,且AO呈水平状态,BO跟竖直方向的夹角为α,那么在剪断AO或BO的瞬间,小球的加速度情况是( )
如图所示,小球用轻质橡皮条AO与不可伸长的细线BO悬吊着,且AO呈水平状态,BO跟竖直方向的夹角为α,那么在剪断AO或BO的瞬间,小球的加速度情况是( )| A. | 剪断AO瞬间,小球加速度大小a=gtanα | |
| B. | 前断AO瞬间,小球加速度大小a=gsinα | |
| C. | 剪断BO瞬间,小球加速度大小a=$\frac{g}{cosα}$ | |
| D. | 不管剪断哪一根,小球加速度均是零 |
12.关于机械振动和机械波的关系,以下说法中正确的是( )
| A. | 有机械振动必有机械波 | |
| B. | 波源振动时的运动速度和波的传播速度始终相同 | |
| C. | 机械波传播过程中任一质点的振动频率与波源的频率始终相同 | |
| D. | 一旦波源停止振动,由它激起的机械波也立即停止波动 |
19.阿祥学习有关直线运动的物理概念后,找到小明、小梅和小雪展开了“讨论与交流”活动,他们提出了以下几个观点,你认为正确的是( )
| A. | 物体在某一时刻的瞬时速度就是瞬时速率 | |
| B. | 运动物体在某段时间内位移为零,则其运动速率也一定为零 | |
| C. | 速度变化得越多,加速度就越大 | |
| D. | 速度变化得越快,加速度就越大 |
9. 如图,实线为不知方向的三条电场线,从电场线中M点以相同速度垂直于电场线方向飞出a、b两个带电粒子,其运动轨迹如图中虚线所示,则( )
如图,实线为不知方向的三条电场线,从电场线中M点以相同速度垂直于电场线方向飞出a、b两个带电粒子,其运动轨迹如图中虚线所示,则( )
 如图,实线为不知方向的三条电场线,从电场线中M点以相同速度垂直于电场线方向飞出a、b两个带电粒子,其运动轨迹如图中虚线所示,则( )
如图,实线为不知方向的三条电场线,从电场线中M点以相同速度垂直于电场线方向飞出a、b两个带电粒子,其运动轨迹如图中虚线所示,则( )| A. | a、b的电势能均减小 | |
| B. | a的速度将减小,b的速度将增加 | |
| C. | a的加速度将增加,b的加速度将减小 | |
| D. | 两个带电粒子的动能,一个增大一个减小 |
14.在电场中某点引入电量为q的正电荷,这个电荷受到的电场力为F,则( )
| A. | 在这点引入电量为2q的正电荷时,该点的电场强度将等于$\frac{F}{2q}$ | |
| B. | 在这点引入电量为2q的正电荷时,该电荷受到的电场力仍为F | |
| C. | 在这点引入电量为2e的正离子时,则离子所受的电场力大小为$\frac{2eF}{q}$ | |
| D. | 若将一个电子引入该点,则由于电子带负电,所以该点的电场强度的方向将与在这一点引入正电荷时相反 |
 如图所示,电源电压为6V,并保持不变,当S1、S2闭合,S3断开时,电流表示数为0.5A,则:
如图所示,电源电压为6V,并保持不变,当S1、S2闭合,S3断开时,电流表示数为0.5A,则: 如图所示,用“碰撞实验器”可以验证动量守恒定律,即研究两个小球在轨道水平部分碰撞前后的动量关系.
如图所示,用“碰撞实验器”可以验证动量守恒定律,即研究两个小球在轨道水平部分碰撞前后的动量关系.