题目内容
（16分）如图所示，水平传送带AB长L=12m，始终以速度v=13m/s运转，在传送带最右端B有一个与水平面成37°的斜坡．现将一个质量为m=2.0kg的小木块轻放在传送带的最左端A，小木块运动到B处就立即沿斜坡运动，但速度大小损失1/6；小木块离开坡顶C后，经过t1=0.3s垂直击中竖直挡板D．已知：小木块与传送带的之间的动摩擦因素μ1=0.6，小木块与斜坡之间的动摩擦因素μ2=0.5，重力加速度g=10m/s2．求:
（1）小木块到达传送带右端B时的速度大小
（2）小木块离开坡顶C时的速度大小
（3）小木块在斜坡上运动过程中，摩擦力对木块的冲量大小
（1）小木块到达传送带右端B时的速度大小
（2）小木块离开坡顶C时的速度大小
（3）小木块在斜坡上运动过程中，摩擦力对木块的冲量大小
(1)
(2) 
(3)
(2) (3)试题分析:
解法一：（1）设小木块运动到右端未与皮带共速由动能定理：
，得：
，故小木块运动到右端速度(2)倒过来看：平抛运动：
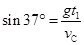，得：(3)设在斜坡上运动时间为
，在斜坡底部速度大小
，得：
由动量定理：
摩擦力的冲量：
解法二：设小木块运动
以后与皮带共速由牛顿第二定律：
②由①②得
，木块滑离B时未与皮带共速。
③ 由①②③得
④(2)
⑤
⑥得
⑦(3)
⑧
⑨
⑩由④⑦⑧⑨⑩得：
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
相关题目
时刻的瞬时速度是
。（g="10" m/s2）求：
