题目内容
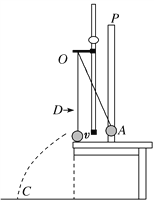
【题目】如图甲所示,两根完全相同的光滑平行导轨固定,每根导轨均由两段与水平面成θ=30°的长直导轨和一段圆弧导轨平滑连接而成,导轨两端均连接电阻,阻值R1=R2=2Ω,导轨间距L=0.6m。在右侧导轨所在斜面的矩形区域M1M2P2P1内分布有垂直斜面向上的磁场,磁场上下边界M1P1、M2P2的距离d=0.2m,磁感应强度大小随时间的变化规律如图乙所示。t=0时刻,在右侧导轨斜面上与M1P1距离s=0.1m处,有一根阻值r=2Ω的金属棒ab垂直于导轨由静止释放,恰好独立匀速通过整个磁场区域,取重力加速度g=10m/s2,导轨电阻不计。求:
(1)ab由静止运动到磁场边界M1P1的时间t及此时的速度大小v;
(2)在t1=0.1s时刻和t2=0.25s时刻电阻R1的电功率之比;

【答案】(1)t=0.2s,v=1m/s;(2) ![]()
【解析】(1)棒从刚开始释放到运动至M1P1这段时间内做匀加速直线运动,设其运动的位移大小是s,时间是t。其运动的加速度大小a由牛顿第二定律可得:ma=mgsinθ ①
由匀变速运动规律可得:s=![]() ②
②
由②③式联立解得:t=0.2(s) ③
由机械能守恒定律可得:mgssinθ=![]() ④
④
由①式解得:v=1(m/s) ⑤(1分)
(2)t1=0.1s时,棒还没有进入磁场,此时由电磁感应规律可得:
![]() ⑥
⑥
此时R2与金属棒并联后再与R1串联,设R1两端的电压U1,由闭合回路欧姆定律可得:
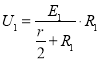 ⑦
⑦
由图乙可知,t1=0.2s后磁场保持不变,ab经过磁场的运动时间:
![]() ⑧
⑧
故当t2=0.25s时,棒ab还在磁场中匀速运动,此时的感应电动势E2:
E2=BLv ⑨
设此时R1两端的电压U1’由闭合回路欧姆定律可得:
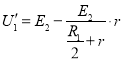 ⑩
⑩
由电功率公式可知电阻R1所消耗的电功率: ![]()
所以在t1=0.1s和t2=0.25s时刻,电阻R1所消耗的电功率之比:
![]()
将数据代入上式解得: ![]()