题目内容
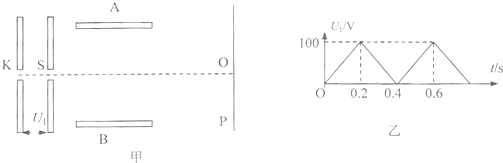
如图甲所示,真空中的电极K连续不断地发出电子(电子的初速度可忽略不计),经电压为Ul的电场加速,加速电压Ul随时间t变化的图象如图乙所示.每个电子通过加速电场的过程时间极短,可认为加速电压不变.电子被加速后由小孔S从穿出,设每秒K向加速电场发射的电子数目恒定.出加速电场后,电子沿两个彼此靠近且正对的水平金属板A、B间中轴线射入偏转电场,A、B两板长均为L=0.20m,两板之间距离d=0.40m,A板的电势比B板的电势高.A,B板右側边缘到竖直放置的荧光屏P(面积足够大)之间的距离b=0.20m.荧光屏的中心点O与A、B板的中心轴线在同一水平直线上.不计电子之间的相互作用力及其所受的重力,求:
(l)要使电子都打不到荧光屏上,则A,B两板间所加电压U2应满足什么条件;
(2)当A、B板间所加电U2=200V时,打到荧光屏上的电子距离中心点O在多大的范围内;
(3)在A、B间加适当的电压,在较长时间内可以使从加速电场中出来的电子90%都能打在荧光屏上,则此情况下所有能打到屏上的电子的动能的最小值为多少.
(l)要使电子都打不到荧光屏上,则A,B两板间所加电压U2应满足什么条件;
(2)当A、B板间所加电U2=200V时,打到荧光屏上的电子距离中心点O在多大的范围内;
(3)在A、B间加适当的电压,在较长时间内可以使从加速电场中出来的电子90%都能打在荧光屏上,则此情况下所有能打到屏上的电子的动能的最小值为多少.

分析:(1)电子做类平抛运动,根据动能定理与运动学公式,即可求解;
(2)电子做类平抛运动,根据侧移量,结合几何关系,可求出最大范围;由U1越大y越小,根据运动学公式可求出最小范围,从而即可求解;
(3)由只要使10V-100V的加速电压下的电子都能打到屏上,就满足了电子都能打在荧光屏上条件.根据运动学公式,得出
=20V时,打在屏上动能最小,从而即可求解.
(2)电子做类平抛运动,根据侧移量,结合几何关系,可求出最大范围;由U1越大y越小,根据运动学公式可求出最小范围,从而即可求解;
(3)由只要使10V-100V的加速电压下的电子都能打到屏上,就满足了电子都能打在荧光屏上条件.根据运动学公式,得出
| U | ′ 1 |
解答:解:(1)设电子的质量为m,电量为e,电子通过加速电场后的速度为v0,
由动能定理有:eU1=
m
电子通过偏转电场的时间t=
此过程中电子的侧向位移y=
at2=
(
)2
解得:y=
要使电子都打不到屏上,应满足U1取最大值100V时仍有y>0.5d
代入数据可得,为使电子都打不到屏上,U2至少为800V.
(2)当电子恰好从A板右边缘射出偏转电场时,
其侧移最大ymax=0.5d=0.2m电子飞出偏转电场时,
其速度的反向延长线通过偏转电场的中心,
设电子打在屏上距中心点的最大距离为,
则由几何关系可得,
=
解得Ymax=
ymax=0.6m
由第(1)问中的y=
可知,在其它条件不变的情况下,U1越大y越小,
所以当U1=100V时,电子通过偏转电场的侧移量最小,
其最小侧移量,ymin=
=0.05m
同理,电子打在屏上距中心的最小距离Ymin=
ymin=0.15m
所以电子打在屏上距中心点O在0.15m~0.6m范围内.
(3)使从加速电场中出来的电子都能打在荧光屏上,则必需使10%的电子落在极板上,对加速电压100V×10%可知,
只要使10V-100V的加速电压下的电子都能打到屏上,就满足了电子都能打在荧光屏上条件.
由y=
=
(
)2=
对U1=10V时还能打到屏上,偏转电压应该U2=80V
打到屏上电子的动能EK=e
+e
y
上式中U2=80V,
为10V-100V范围中的某一电压
y=
(
)2=
=
EK=e
+e
y=e(
+
)
则当
=
时,即
=20V时,打在屏上动能最小,最小EK=40eV
答:(l)要使电子都打不到荧光屏上,则A,B两板间所加电压U2应满足至少为800V条件;
(2)当A、B板间所加电U2=200V时,打到荧光屏上的电子距离中心点O在0.15m~0.6m的范围内;
(3)在A、B间加适当的电压,在较长时间内可以使从加速电场中出来的电子90%都能打在荧光屏上,则此情况下所有能打到屏上的电子的动能的最小值为40eV.
由动能定理有:eU1=
| 1 |
| 2 |
| v | 2 0 |
电子通过偏转电场的时间t=
| L |
| v0 |
此过程中电子的侧向位移y=
| 1 |
| 2 |
| 1 |
| 2 |
| eU2 |
| dm |
| L |
| v0 |
解得:y=
| U2L2 |
| 4dU1 |
要使电子都打不到屏上,应满足U1取最大值100V时仍有y>0.5d
代入数据可得,为使电子都打不到屏上,U2至少为800V.
(2)当电子恰好从A板右边缘射出偏转电场时,
其侧移最大ymax=0.5d=0.2m电子飞出偏转电场时,
其速度的反向延长线通过偏转电场的中心,
设电子打在屏上距中心点的最大距离为,
则由几何关系可得,
| Ymax |
| ymax |
b+
| ||
|
解得Ymax=
b+
| ||
|
由第(1)问中的y=
| U2L2 |
| 4dU1 |
所以当U1=100V时,电子通过偏转电场的侧移量最小,
其最小侧移量,ymin=
| U1L2 |
| 4dU1 |
同理,电子打在屏上距中心的最小距离Ymin=
b+
| ||
|
所以电子打在屏上距中心点O在0.15m~0.6m范围内.
(3)使从加速电场中出来的电子都能打在荧光屏上,则必需使10%的电子落在极板上,对加速电压100V×10%可知,
只要使10V-100V的加速电压下的电子都能打到屏上,就满足了电子都能打在荧光屏上条件.
由y=
| d |
| 2 |
| 1 |
| 2 |
| eU2 |
| dm |
| L |
| v0 |
| U2L2 |
| 4dU1 |
对U1=10V时还能打到屏上,偏转电压应该U2=80V
打到屏上电子的动能EK=e
| U | ′ 1 |
| U2 |
| d |
上式中U2=80V,
| U | ′ 1 |
y=
| 1 |
| 2 |
| eU2 |
| dm |
| L |
| v0 |
| U2L2 | ||
4d
|
| 2 | ||
|
EK=e
| U | ′ 1 |
| U2 |
| d |
| U | ′ 1 |
| 400 | ||
|
则当
| U | ′ 1 |
| 400 | ||
|
| U | ′ 1 |
答:(l)要使电子都打不到荧光屏上,则A,B两板间所加电压U2应满足至少为800V条件;
(2)当A、B板间所加电U2=200V时,打到荧光屏上的电子距离中心点O在0.15m~0.6m的范围内;
(3)在A、B间加适当的电压,在较长时间内可以使从加速电场中出来的电子90%都能打在荧光屏上,则此情况下所有能打到屏上的电子的动能的最小值为40eV.
点评:考查电子在电场中做类平抛运动,学会运动的分解,并根据运动学公式与牛顿第二定律及动能定理综合解题,强调电子在不同的电场中的运动与受力情况.

练习册系列答案
相关题目

 [选做题]本题包括A、B、C三小题,请选定其中两题,并在相应的答题区域内作答.若三题都做,则按A、B两题评分.
[选做题]本题包括A、B、C三小题,请选定其中两题,并在相应的答题区域内作答.若三题都做,则按A、B两题评分.
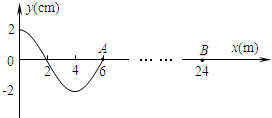
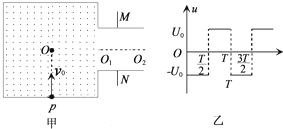 如图甲所示,在真空中,有一边长为a的正方形区域内存在匀强磁场,磁场方向垂直纸面向外.在磁场右侧有一对平行金属板M和N,两板间距及板长均为b,板间的中心线O1O2与正方形的中心O在同一直线上.有一电荷量为q、质量为m的带正电的粒子以速度v0从正方形的底边中点P沿PO方向进入磁场,从正方形右侧O1点水平飞出磁场时,立即给M、N两板加上如图乙所示的交变电压,最后粒子刚好以平行于M板的速度从M板的边缘飞出.(不计粒子所受到的重力、两板正对面之间为匀强电场,边缘电场不计)
如图甲所示,在真空中,有一边长为a的正方形区域内存在匀强磁场,磁场方向垂直纸面向外.在磁场右侧有一对平行金属板M和N,两板间距及板长均为b,板间的中心线O1O2与正方形的中心O在同一直线上.有一电荷量为q、质量为m的带正电的粒子以速度v0从正方形的底边中点P沿PO方向进入磁场,从正方形右侧O1点水平飞出磁场时,立即给M、N两板加上如图乙所示的交变电压,最后粒子刚好以平行于M板的速度从M板的边缘飞出.(不计粒子所受到的重力、两板正对面之间为匀强电场,边缘电场不计) 
