题目内容
5．竖直悬挂的弹簧下端，挂一重为3N的物体时，弹簧长度为12cm；挂重为6N的物体时，弹簧长度为15cm，则弹簧的原长为多少，劲度系数为多少．分析 物体静止时，弹簧的弹力等于所悬挂物体的重力，弹簧伸长的长度等于弹簧的长度减去原长．根据胡克定律对两种情况分别列方程求解劲度系数k．
解答 解：l1=12cm=0.12m，l2=13cm=0.13m
设弹簧的劲度系数k，原长为l0．根据胡克定律得：
当挂重为4N的物体时，G1=k（l1-l0）…①
当挂重为6N的物体时，G2=k（l2-l0）…②
联立得：l0=0.1m=10cm；k=200N/m
答：（1）弹簧的原长为10cm．
（2）弹簧的劲度系数200N/m
点评 本题是胡定定律的基本应用，抓住公式F=kx中x是弹簧伸长的长度或压缩的长度．
练习册系列答案
智趣暑假温故知新系列答案
相关题目
15．
一列简谐横波在x轴上传播．t=0时的波形图如图所示，质点A与质点B相距1m，A点速度沿y轴的正方向；t=0.02s时，质点A第一次到达正向最大位移处．由此可知（ ）
一列简谐横波在x轴上传播．t=0时的波形图如图所示，质点A与质点B相距1m，A点速度沿y轴的正方向；t=0.02s时，质点A第一次到达正向最大位移处．由此可知（ ）| A． | 此波的传播速度为25m/s | |
| B． | 从t=0时刻起，经过0.04s，质点A沿波的传播方向迁移了1m | |
| C． | 在t=0.04s时，质点B处在平衡位置，速度沿y轴负方向 | |
| D． | 若此波遇到另一列波并发生稳定干涉现象，则另一列波的频率为12.5Hz |
16．
如图所示，将一质量为m的小球从空中o点以速度v0水平抛出，飞行一段时间后，小球经过P点时动能Ek=5mv02，不计空气阻力，则小球从O到P（ ）
如图所示，将一质量为m的小球从空中o点以速度v0水平抛出，飞行一段时间后，小球经过P点时动能Ek=5mv02，不计空气阻力，则小球从O到P（ ）| A． | 下落的高度为$\frac{5{{v}_{0}}^{2}}{g}$ | B． | 经过的时间为$\frac{2{v}_{0}}{g}$ | ||
| C． | 运动方向改变的角度为arctan$\frac{1}{3}$ | D． | 速度增量为3v0，方向竖直向下 |
13．下列是某同学对电场中的概念、公式的理解，其中正确的是（ ）
| A． | 根据电场强度的定义式E=$\frac{F}{q}$，电场中某点的电场强度和试探电荷的电量成反比 | |
| B． | 电场中两点的电势差是确定的，与零势能面的选取有关 | |
| C． | 根据真空中点电荷电场强度公式E=k$\frac{Q}{{r}^{2}}$，电场中某点电场强度和场源电荷的电量无关 | |
| D． | 电场中某点的电势与参考平面的选取有关 |
20．据最新报道，放射性同位素钬${\;}_{67}^{166}$Ho，可有效治疗癌症，该同位素原子核内中子数与核外电子数之差是（ ）
| A． | 32 | B． | 67 | C． | 99 | D． | 166 |
10．
如图为玻璃自动切割生产线示意图．图中，玻璃以恒定的速度v向右运动，两侧的滑轨与玻璃的运动方向平行．滑杆与滑轨垂直，且可沿滑轨左右移动．割刀通过沿滑杆滑动和随滑杆左右移动实现对移动玻璃的切割．移动玻璃的宽度为L，要使切割后的玻璃为长2L的矩形，以下做法能达到要求的是（ ）
如图为玻璃自动切割生产线示意图．图中，玻璃以恒定的速度v向右运动，两侧的滑轨与玻璃的运动方向平行．滑杆与滑轨垂直，且可沿滑轨左右移动．割刀通过沿滑杆滑动和随滑杆左右移动实现对移动玻璃的切割．移动玻璃的宽度为L，要使切割后的玻璃为长2L的矩形，以下做法能达到要求的是（ ）| A． | 保持滑杆不动，使割刀以速度$\frac{v}{2}$沿滑杆滑动 | |
| B． | 滑杆以速度v向左移动的同时，割刀以速度$\frac{v}{2}$沿滑杆滑动 | |
| C． | 滑杆以速度v向右移动的同时，割刀以速度2v沿滑杆滑动 | |
| D． | 滑杆以速度v向右移动的同时，割刀以速度$\frac{v}{2}$沿滑杆滑动 |
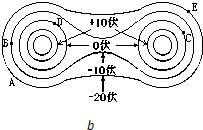如图所示，是一组两个平行带电圆柱垂直平面的等势线，在图中标出了各等势线的电势数值．试求：