题目内容
9.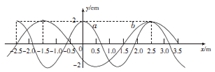 a、b两列简谐横波在同一介质中沿x轴正方向传播,波速均为v=2.5m/s,在t=0时,两列波的波形如图所示,下列说法正确的是( )
a、b两列简谐横波在同一介质中沿x轴正方向传播,波速均为v=2.5m/s,在t=0时,两列波的波形如图所示,下列说法正确的是( )| A. | a、b两列波的波长之比是5:8 | |
| B. | a、b两列波叠加时能形成稳定的干涉图样 | |
| C. | t=0时平衡位置在x=2.5m处 的位移为4cm | |
| D. | t=0时平衡位置在x=1.5m处的质点沿y轴正方向运动 | |
| E. | t=8s时介质中各质点的位置与t=0时的位置相同 |
分析 由图直接读出两列波的波长,再求得波长之比.两列性质相同的简谐横波a、b在同一介质中传播时波速是相同的,由波速公式分析它们频率关系,再判断能否两列叠加时能否产生稳定的干涉.根据波的叠加原理分析质点的位移.由波的传播方向判断质点的振动方向.根据时间与周期的关系分析t=8s时介质中各质点的位置与t=0时的位置关系.
解答 解:A、从图中可以看出两列波的波长分别为 λa=2.5m,λb=4.0m,则波长之比 λa:λb=5:8,故A正确.
B、两列性质相同的简谐横波a、b在同一介质中传播时波速是相等的,根据v=λf知,它们的波长不等,则频率不等,因此a、b两列波叠加时不能形成稳定的干涉图样.故B错误.
C、t=0时平衡位置在x=2.5m处是两列波的波峰相遇处,由波的叠加原理知,该点的位移 y=2A=2×2cm=4cm,故C正确.
D、根据波形平移法可知,a、b两波单独传播时平衡位置在x=1.5m处的质点均沿y轴负方向运动,由波的叠加原理可知,t=0时平衡位置在x=1.5m处的质点沿y轴负方向.故D错误.
E、a、b两波周期分别为 Ta=$\frac{{λ}_{a}}{v}$=$\frac{2.5}{2.5}$=1s,Tb=$\frac{{λ}_{b}}{v}$=$\frac{4}{2.5}$=1.6s,由于t=8s=8Ta=5Tb,而波每经过一个周期时介质中各质点状态重复,所以t=8s时介质中各质点的位置与t=0时的位置相同,故E正确.
故选:ACE
点评 解决本题的关键是理解并掌握波的叠加原理,知道波的周期性即重复性,能熟练运用波形平移法分析质点的振动方向.

练习册系列答案
相关题目
19.一质量为2kg的物体在5个共点力作用下做匀速直线运动.现撤去其中一个大小为10N的力,其余的力大小和方向均保持不变.下列关于此后该物体运动的说法中,正确的是( )
| A. | 可能做匀减速直线运动,加速度大小为5 m/s2 | |
| B. | 可能做匀速圆周运动,向心加速度大小为5 m/s2 | |
| C. | 可能做匀变速曲线运动,加速度大小为5 m/s2 | |
| D. | 一定做匀变速直线运动,加速度大小为5 m/s2 |
4.地球可视为一个磁偶极,其中一个极位于地理北极附近,另一极位于地理南极附近.下列说法正确的是( )
| A. | 地磁场是匀强磁场 | |
| B. | 地磁场的南极在地球的南极附近 | |
| C. | 地磁场的北极在地球的南极附近 | |
| D. | 在地区的北极处,地磁场是竖直向上的 |
14.科学家们通过大量的实践研究,估算出了整个地球表面接受的太阳辐射能主要去向的数据:
根据以上数据可估算出地球对太阳能的利用率为23.7%,每年通过植物的光合作用转化的化学能为1.57×1018kJ(两空均保留三位数).
| 直接反射 | 以热辐射形式散发到太空 | 水循环 | 大气流动 | 光合作用 |
| 5.0×1013kJ/s | 8.0×1013kJ/s | 4.0×1013kJ/s | 4.0×1011kJ/s | 5.0×1010kJ/s |
1.以下说法中正确的是( )
| A. | 光波是概率波,物质波不是概率波 | |
| B. | 实物粒子不具有波动性 | |
| C. | 实物粒子也具有波动性,只是不明显 | |
| D. | 光的波动性是光子之间相互作用引起的 |
18.如图所示,下列实验中,深入地揭示了光的粒子性一面的是( )
| A. |  光的双缝干涉 | |
| B. |  光电效应 | |
| C. |  α粒子散射实验 | |
| D. |  光的单缝衍射 | |
| E. |  康普顿效应 |
17.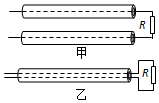 应用物理知识分析生活中的常见现象,可以使物理学习更加有趣和深入.某输电线路横穿公路时,要在地下埋线.为了保护输电线不至于被压坏,可预先铺设结实的过路钢管,再让输电线从钢管中穿过.电线穿过钢管的方案有两种(如图所示):甲方案是铺设两根钢管,两条输电线分别从两根钢管中穿过;乙方案是只铺设一根钢管,两条输电线都从这一根钢管中穿过.如果输电导线输送的电流很强大,为了减小电磁感应带来的不利影响,那么以下说法正确的是( )
应用物理知识分析生活中的常见现象,可以使物理学习更加有趣和深入.某输电线路横穿公路时,要在地下埋线.为了保护输电线不至于被压坏,可预先铺设结实的过路钢管,再让输电线从钢管中穿过.电线穿过钢管的方案有两种(如图所示):甲方案是铺设两根钢管,两条输电线分别从两根钢管中穿过;乙方案是只铺设一根钢管,两条输电线都从这一根钢管中穿过.如果输电导线输送的电流很强大,为了减小电磁感应带来的不利影响,那么以下说法正确的是( )
 应用物理知识分析生活中的常见现象,可以使物理学习更加有趣和深入.某输电线路横穿公路时,要在地下埋线.为了保护输电线不至于被压坏,可预先铺设结实的过路钢管,再让输电线从钢管中穿过.电线穿过钢管的方案有两种(如图所示):甲方案是铺设两根钢管,两条输电线分别从两根钢管中穿过;乙方案是只铺设一根钢管,两条输电线都从这一根钢管中穿过.如果输电导线输送的电流很强大,为了减小电磁感应带来的不利影响,那么以下说法正确的是( )
应用物理知识分析生活中的常见现象,可以使物理学习更加有趣和深入.某输电线路横穿公路时,要在地下埋线.为了保护输电线不至于被压坏,可预先铺设结实的过路钢管,再让输电线从钢管中穿过.电线穿过钢管的方案有两种(如图所示):甲方案是铺设两根钢管,两条输电线分别从两根钢管中穿过;乙方案是只铺设一根钢管,两条输电线都从这一根钢管中穿过.如果输电导线输送的电流很强大,为了减小电磁感应带来的不利影响,那么以下说法正确的是( )| A. | 无论输送的电流是恒定电流还是交变电流,甲、乙两方案都是可行的 | |
| B. | 若输送的电流是交变电流,甲、乙两方案都是可行的 | |
| C. | 若输送的电流是交变电流,甲方案是不可行的,乙方案是可行的 | |
| D. | 若输送的电流是交变电流,甲方案是可行的,乙方案是不可行的 |
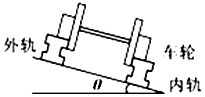 铁路在弯道处的内外轨道高低是不同的,已知内外轨道对水平面倾角为θ,如图所示,弯道处的圆弧半径为R,若质量为m的火车转弯时速度等于$\sqrt{gRtanθ}$,则火车不挤压内外轨道,若速度大于$\sqrt{gRtanθ}$则火车挤压外轨道,若速度小于$\sqrt{gRtanθ}$则火车挤压内轨道.(填“内”或“外”)
铁路在弯道处的内外轨道高低是不同的,已知内外轨道对水平面倾角为θ,如图所示,弯道处的圆弧半径为R,若质量为m的火车转弯时速度等于$\sqrt{gRtanθ}$,则火车不挤压内外轨道,若速度大于$\sqrt{gRtanθ}$则火车挤压外轨道,若速度小于$\sqrt{gRtanθ}$则火车挤压内轨道.(填“内”或“外”)