题目内容
某同学用单摆测重力加速度，测完了5次不同摆长的振动周期，数据如下：| 摆长L/m | 0.500 | 0.800 | 0.900 | 1.000 | 1.200 |
| 周期T/s | 1.42 | 1.78 | 1.90 | 2.00 | 2.20 |
| T2/s2 | 2.02 | 3.17 | 3.61 | 4.00 | 4.84 |
（2）利用图象求出重力加速度g的值（保留三位有效数字，π2=9.87），g=
9.87
9.87
m/s2．分析：（1）应用描点法作图，根据表中实验数据，在坐标纸上描出相应的点，然后把各点连接起来，即可作出图象．
（2）由单摆周期公式的变形公式求出T2-L关系表达式，然后根据图象求出重力加速度．
（2）由单摆周期公式的变形公式求出T2-L关系表达式，然后根据图象求出重力加速度．
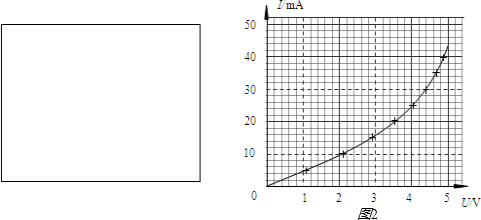
解答：
解：（1）应用描点法作图，作出l-T2图象如图所示．
（2）T=2π
可知，L=
T2=kT2，其中k=
，
g=4kπ2，由图象可知，斜率k=0.25，
则重力加速度：g=4kπ2=4×0.25×9.87=9.87m/s2；
故答案为：（1）图象如图所示；（2）9.87．
解：（1）应用描点法作图，作出l-T2图象如图所示．（2）T=2π
|
| g |
| 4π2 |
| g |
| 4π2 |
g=4kπ2，由图象可知，斜率k=0.25，
则重力加速度：g=4kπ2=4×0.25×9.87=9.87m/s2；
故答案为：（1）图象如图所示；（2）9.87．
点评：根据表中实验数据应用描点法作图是正确解题的关键，由图象求出图象的斜率，应用周期公式是变形公式，即可求出重力加速度．
练习册系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
在用单摆测重力加速度的实验中，某同学测出不同摆长时对应的周期T，作出L-T2图线，如图所示，再利用图线上任意两点A、B的坐标（x1，y1）、（x2，y2），可求得g=
（2009?杨浦区模拟）在用单摆测重力加速度的实验中：
；
