题目内容
11.某行星绕太阳运动的轨道如图所示,则以下说法不正确的是( )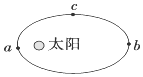
| A. | 太阳一定在椭圆的一个焦点上 | |
| B. | 该行星在a点的速度比在b、c两点的速度都大 | |
| C. | 该行星在c点的速度比在a、b两点的速度都大 | |
| D. | 行星与太阳的连线在相等时间内扫过的面积是相等的 |
分析 开普勒的行星运动三定律:
第一定律:所有的行星围绕太阳运动的轨道都是椭圆,太阳处在所有椭圆的一个焦点上.
第二定律:对每一个行星而言,太阳行星的连线在相同时间内扫过的面积相等.
第三定律:所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等
解答 解:A、行星围绕太阳运动的轨道都是椭圆,太阳处在所有椭圆的一个焦点上,则A正确
B、C、D、每一个行星而言,太阳行星的连线在相同时间内扫过的面积相等,即近日点速度快,远日点速度慢,则B正确,C错误,D正确
因选错误的,故选:C
点评 明确开普勒定律的内容,是其基本的应用,不难.

练习册系列答案
相关题目
19.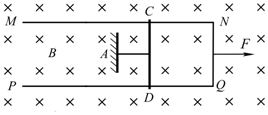 如图所示,一个质量为m、电阻不计、足够长的光滑U形金属框架MNQP,位于光滑绝缘水平桌面上,平行导轨MN和PQ相距为L.空间存在着足够大的方向竖直向下的匀强磁场,磁感应强度的大小为B.另有质量也为m的金属棒CD,垂直于MN放置在导轨上,并用一根绝缘细线系在定点A.已知,细线能承受的最大拉力为T0,CD棒接入导轨间的有效电阻为R.现从t=0时刻开始对U形框架施加水平向右的拉力,使其从静止开始做加速度为a的匀加速直线运动,经过一段时间后,细线断裂,在细线断裂时,立即撤去拉力,关于撤去拉力前后的全过程,下列说法正确的是( )
如图所示,一个质量为m、电阻不计、足够长的光滑U形金属框架MNQP,位于光滑绝缘水平桌面上,平行导轨MN和PQ相距为L.空间存在着足够大的方向竖直向下的匀强磁场,磁感应强度的大小为B.另有质量也为m的金属棒CD,垂直于MN放置在导轨上,并用一根绝缘细线系在定点A.已知,细线能承受的最大拉力为T0,CD棒接入导轨间的有效电阻为R.现从t=0时刻开始对U形框架施加水平向右的拉力,使其从静止开始做加速度为a的匀加速直线运动,经过一段时间后,细线断裂,在细线断裂时,立即撤去拉力,关于撤去拉力前后的全过程,下列说法正确的是( )
 如图所示,一个质量为m、电阻不计、足够长的光滑U形金属框架MNQP,位于光滑绝缘水平桌面上,平行导轨MN和PQ相距为L.空间存在着足够大的方向竖直向下的匀强磁场,磁感应强度的大小为B.另有质量也为m的金属棒CD,垂直于MN放置在导轨上,并用一根绝缘细线系在定点A.已知,细线能承受的最大拉力为T0,CD棒接入导轨间的有效电阻为R.现从t=0时刻开始对U形框架施加水平向右的拉力,使其从静止开始做加速度为a的匀加速直线运动,经过一段时间后,细线断裂,在细线断裂时,立即撤去拉力,关于撤去拉力前后的全过程,下列说法正确的是( )
如图所示,一个质量为m、电阻不计、足够长的光滑U形金属框架MNQP,位于光滑绝缘水平桌面上,平行导轨MN和PQ相距为L.空间存在着足够大的方向竖直向下的匀强磁场,磁感应强度的大小为B.另有质量也为m的金属棒CD,垂直于MN放置在导轨上,并用一根绝缘细线系在定点A.已知,细线能承受的最大拉力为T0,CD棒接入导轨间的有效电阻为R.现从t=0时刻开始对U形框架施加水平向右的拉力,使其从静止开始做加速度为a的匀加速直线运动,经过一段时间后,细线断裂,在细线断裂时,立即撤去拉力,关于撤去拉力前后的全过程,下列说法正确的是( )| A. | 撤去拉力F,框架的速度v0=$\frac{{T}_{0}R}{{{B}^{2}L}^{2}}$ | |
| B. | 从框架开始运动到细线断裂所需的时间t0=$\frac{{T}_{0}R}{{{B}^{2}L}^{2}a}$ | |
| C. | 撤去拉力后,框架将向右减速,棒向右加速,二者最终速度相同 | |
| D. | 最终在回路中产生的总焦耳热等于拉力F做的功 |
3. 两块水平放置的金属板与电键K、线圈如图所示连接,两板间放有一与板绝缘的压力传感器,其上表面静置一个质量为m、电量为+q的小球,两板间距离为d,线圈匝数为n.开始时K断开,然后将线圈置于方向竖直向上的变化磁场B中,再闭合K,发现传感器示数为零.则对磁场B的变化情况和磁通量变化率正确的判断是( )
两块水平放置的金属板与电键K、线圈如图所示连接,两板间放有一与板绝缘的压力传感器,其上表面静置一个质量为m、电量为+q的小球,两板间距离为d,线圈匝数为n.开始时K断开,然后将线圈置于方向竖直向上的变化磁场B中,再闭合K,发现传感器示数为零.则对磁场B的变化情况和磁通量变化率正确的判断是( )
 两块水平放置的金属板与电键K、线圈如图所示连接,两板间放有一与板绝缘的压力传感器,其上表面静置一个质量为m、电量为+q的小球,两板间距离为d,线圈匝数为n.开始时K断开,然后将线圈置于方向竖直向上的变化磁场B中,再闭合K,发现传感器示数为零.则对磁场B的变化情况和磁通量变化率正确的判断是( )
两块水平放置的金属板与电键K、线圈如图所示连接,两板间放有一与板绝缘的压力传感器,其上表面静置一个质量为m、电量为+q的小球,两板间距离为d,线圈匝数为n.开始时K断开,然后将线圈置于方向竖直向上的变化磁场B中,再闭合K,发现传感器示数为零.则对磁场B的变化情况和磁通量变化率正确的判断是( )| A. | 正在增加,$\frac{△ϕ}{△t}=\frac{mgd}{q}$ | B. | 正在减弱,$\frac{△ϕ}{△t}=\frac{mgd}{nq}$ | ||
| C. | 正在减弱,$\frac{△ϕ}{△t}=\frac{mgd}{q}$ | D. | 正在增加,$\frac{△ϕ}{△t}=\frac{mgd}{nq}$ |
6.2016年8月16日1时40时,我国在酒泉卫星发射中心成功将世界首颗量子卫星“墨子号”发射升空,在距离地面高度为h的轨道上运行.设火箭点火后在时间t内竖直向上匀加速飞行,匀加速过程的末速度为v,这一过程对应的质量为m,认为“墨子号”最终在轨道上做匀速圆周运动,地球的半径为R,地球表面的重力加速度为g,引力常量为G,忽略时间t内火箭的质量变化,不考虑空气阻力的影响,下列说法正确的是( )
| A. | 火箭竖直向上匀加速过程中的推力为$\frac{mv}{t}$ | |
| B. | 火箭竖直向上匀加速飞行的过程中克服重力做功的平均功率为mgv | |
| C. | 地球的平均密度为 $\frac{3g}{4πGR}$ | |
| D. | “墨子号”在最终轨道上绕地球运行的周期为$\frac{2m(R+h)}{R}\sqrt{\frac{R+h}{g}}$ |
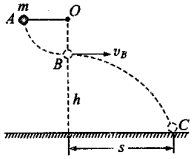 如图所示,轻绳一端固定在O点,另一端系住质量m=1.0kg的小球(可视为质点),A点与O点位于同一水平高度.小球从A点由静止释放后在竖直平面内做圆周运动,到达O点正下方的B点时绳子突然断裂,小球从B点开始做平抛运动并落在水平面上的C点,B点与水平面的高度差h=1.8m,B、C间的水平距离s=2.4m,O、A、B、C在同一竖直面内,重力加速度g取10m/s2,不计一切阻力.求:
如图所示,轻绳一端固定在O点,另一端系住质量m=1.0kg的小球(可视为质点),A点与O点位于同一水平高度.小球从A点由静止释放后在竖直平面内做圆周运动,到达O点正下方的B点时绳子突然断裂,小球从B点开始做平抛运动并落在水平面上的C点,B点与水平面的高度差h=1.8m,B、C间的水平距离s=2.4m,O、A、B、C在同一竖直面内,重力加速度g取10m/s2,不计一切阻力.求: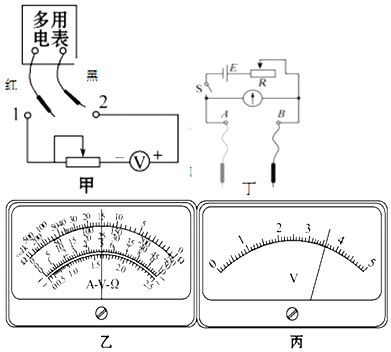
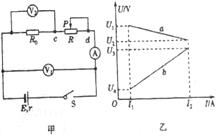 某同学利用如图甲所示电路测定电源的电动势和内阻,闭合开关S后,变阻器的滑片P由变阻器的一端滑到另一端的过程,两电压表示数随电流表示数变化情况分别如图乙所示的U-I图象中的直线a、b所示,根据U-I图象中坐标轴所标了的数据,计算或回答下列问题:
某同学利用如图甲所示电路测定电源的电动势和内阻,闭合开关S后,变阻器的滑片P由变阻器的一端滑到另一端的过程,两电压表示数随电流表示数变化情况分别如图乙所示的U-I图象中的直线a、b所示,根据U-I图象中坐标轴所标了的数据,计算或回答下列问题: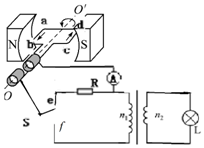 如图,矩形线框匝数为n=250,ab=12cm,cd=10cm,线框置于B=$\frac{2}{π}$T的匀强电场中,绕垂直于磁场的轴以120r/min的转速匀速转动,线框通过滑环与外电路相连,外电路有R=12Ω的电阻及变压器和一只“24$\sqrt{2}$V、34Ω”的灯泡L(线框电阻不计).求:
如图,矩形线框匝数为n=250,ab=12cm,cd=10cm,线框置于B=$\frac{2}{π}$T的匀强电场中,绕垂直于磁场的轴以120r/min的转速匀速转动,线框通过滑环与外电路相连,外电路有R=12Ω的电阻及变压器和一只“24$\sqrt{2}$V、34Ω”的灯泡L(线框电阻不计).求: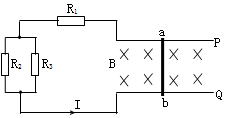 如图所示P、Q为光滑的平行金属导轨(其电阻可忽略不计),导轨间距为0.5m.已知垂直纸面向里的匀强磁场的磁感应强度B=1T,R1=2.5Ω,R2=R3=8Ω,通过电路的电流方向如图所示,导体棒ab的电阻为0.5Ω.当导体棒沿导轨P、Q以某一速度运动时,R2消耗的功率为0.5W.求:
如图所示P、Q为光滑的平行金属导轨(其电阻可忽略不计),导轨间距为0.5m.已知垂直纸面向里的匀强磁场的磁感应强度B=1T,R1=2.5Ω,R2=R3=8Ω,通过电路的电流方向如图所示,导体棒ab的电阻为0.5Ω.当导体棒沿导轨P、Q以某一速度运动时,R2消耗的功率为0.5W.求: