题目内容
两质量相同的物体a和b分别静止在光滑的水平桌面上,因分别受到水平恒力作用,同时开始运动.若b所受的力为a的k倍,经过t时间后分别用Ia、Wb;Wa和Ib、Wb表示在这段时间内a和b各自所受恒力的冲量和做功的大小,则有( )A.Wb=kWa,Ib=kIa
B.Wb=k2Wa,Ib=kIa
C.Wb=kWa,Ib=k2Ia
D.Wb=k2Wa,Ib=k2Ia
【答案】分析:冲量I=Ft,而力做功W=FS;则由冲量定理可求得恒力的冲量;由运动学公式可求得物体在t内的位移,则可由功的公式求出恒力所做的功.
解答:解:因冲量I=Ft,两物体运动时间相同,b受到力为a受力的k倍,由I=Ft可知,b的冲量为a冲量的k倍;即Ib=kIa;
物体在恒力的作用下做匀加速直线运动,则ts内的位移s= at2=
at2=
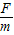 t2;
t2;
则力做功W=Fs=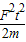 ;
;
故外力做功Wb=k2Wa;
故选B.
点评:本题要求学生掌握求冲量及冲功的方法,要注意正确掌握相应的规律.
解答:解:因冲量I=Ft,两物体运动时间相同,b受到力为a受力的k倍,由I=Ft可知,b的冲量为a冲量的k倍;即Ib=kIa;
物体在恒力的作用下做匀加速直线运动,则ts内的位移s=
 at2=
at2=
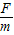 t2;
t2;则力做功W=Fs=
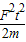 ;
;故外力做功Wb=k2Wa;
故选B.
点评:本题要求学生掌握求冲量及冲功的方法,要注意正确掌握相应的规律.

练习册系列答案
相关题目