��Ŀ����
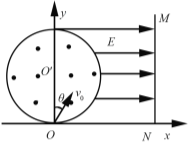
����Ŀ����18�֣���ͼ��ʾ����ֱ������ϵxOyƽ������һ�뾶ΪR��Բ��ΪO'(0��R)��Բ������Բ�������ڴ����ŷ���ֱԲ�����⡢�Ÿ�Ӧǿ�ȴ�СΪB����ǿ�ų���Բ�������Ҳ���һ������x�����������ǿ�糡����ǿ��СE=![]() ���̶���Ե��MN��ֱ��x������y���ľ���Ϊ
���̶���Ե��MN��ֱ��x������y���ľ���Ϊ![]() R��һ����Ϊm�������Ϊq�Ĵ��������ӣ�������������������ԭ��O�Դ�СΪv0=
R��һ����Ϊm�������Ϊq�Ĵ��������ӣ�������������������ԭ��O�Դ�СΪv0=![]() ��������y��������нǦ�=37����ٶȴ�ֱ�ų������һ���ޣ�����ų������糡����MN������ײ����ײǰ����y�᷽��ķ��ٶȲ��䣬��x�᷽��ķ��ٶȴ�С���䡢������ȡsin 37��=0.6��cos 37��=0.8����
��������y��������нǦ�=37����ٶȴ�ֱ�ų������һ���ޣ�����ų������糡����MN������ײ����ײǰ����y�᷽��ķ��ٶȲ��䣬��x�᷽��ķ��ٶȴ�С���䡢������ȡsin 37��=0.6��cos 37��=0.8����
��1�����ӵ�һ������ų�ʱ��λ��P1�Լ�������MN������ײǰ˲����ٶȴ�Сv��
��2�����ӵڶ�������ų�ʱ��λ��P2�Լ����Ӵӵ�һ������ų������һ������ų������ڴų����˶�����ʱ��t��
���𰸡���1��(![]() R��
R��![]() R)��6�֣� v=
R)��6�֣� v=![]() ��4�֣� ��2��(0��2R)��2�֣� t=
��4�֣� ��2��(0��2R)��2�֣� t=![]() ��6�֣�
��6�֣�
����������1����ͼ��ʾ�����ӵ�һ���ڴų�������O1ΪԲ�ĵ�����Բ���˶�������켣�뾶Ϊr
����qv0B=m![]() ������v0=
������v0=![]() ��2�֣�
��2�֣�
���r=![]() =R��1�֣�
=R��1�֣�
�ɼ����ı���OO1P1O'�����Σ�1�֣�
�ɼ���֪ʶ�����ӹ�P1ʱ���ٶȷ����ص糡����P1������Ϊ(rcos ����r�Crsin ��)��1�֣�
�ɵ�P1������(![]() R��
R��![]() R)��1�֣�
R)��1�֣�
�ڵ���MNǰ�����ڵ糡�����ȼ���ֱ���˶�����v2�Cv02=2a(![]() R�C
R�C![]() R)��2�֣�
R)��2�֣�
����a=![]() ��E=
��E=![]() ��1�֣�
��1�֣�
���v=![]() ��1�֣�
��1�֣�
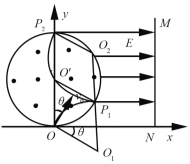
��2�����ӵڶ����ڴų���������Ϊv0��O2ΪԲ�ĵ�����Բ���˶����ı���P1O��P2O2�����Σ��ɼ���֪ʶ��P2������Ϊ(0��2R)��2�֣�
��t=![]() ��2�֣�
��2�֣�
�ɼ��ι�ϵ֪��OO1P1+��P2O2P1=����2�֣�
�ɵ�t=![]() ��2�֣�
��2�֣�

 ��У����ϵ�д�
��У����ϵ�д�