题目内容
 如图所示,ab是半径为R的圆的一条直径,该圆处于匀强电场中,场强大小为E,方向与圆周平面平行.在圆周平面内将质量为m,带正电为q的粒子,从a点同时以相同的动能在圆周平面向各个方向抛出,粒子会经过圆周上不同的点.在这些点中,到达c点的粒子动能最大,已知ac和ab间的夹角θ=30°,若不计重力和空气阻力及粒子间的相互作用力,求:
如图所示,ab是半径为R的圆的一条直径,该圆处于匀强电场中,场强大小为E,方向与圆周平面平行.在圆周平面内将质量为m,带正电为q的粒子,从a点同时以相同的动能在圆周平面向各个方向抛出,粒子会经过圆周上不同的点.在这些点中,到达c点的粒子动能最大,已知ac和ab间的夹角θ=30°,若不计重力和空气阻力及粒子间的相互作用力,求:(1)电场方向与ab间的夹角α为多大?
(2)若粒子在a点时的初速度与电场方向垂直,则粒子恰好能落在C点,则初速度为多大?
(3)若在a点时的初速度与电场方向垂直的粒子恰好落在C点时,是否还有其它粒子同时落到圆周上.若有,求出其它粒子在圆周上的落点到C点的距离;若没有,说明理由.
分析:(1)小球在匀强电场中,从A点运动到C点,根据动能定理qUAC=Ek,因为到达C点时的小球的动能最大,所以UAC最大,即在圆周上找不到与C电势相等的点.所以与C点电势相等的点在过C点的切线上.再根据电场线与等势线垂直,可以画出电场线.
(2)小球做类平抛运动,根据平抛运动的知识分析小球的运动情况,分别在水平方向和竖直方向上列式求解.
(3)通过类比,看成类平抛运动,结合运动学公式与牛顿第二定律,及运动的合成与分解,即可求解.
(2)小球做类平抛运动,根据平抛运动的知识分析小球的运动情况,分别在水平方向和竖直方向上列式求解.
(3)通过类比,看成类平抛运动,结合运动学公式与牛顿第二定律,及运动的合成与分解,即可求解.
解答:解:(1)小球在匀强电场中,从a点运动到c点,根据动能定理qUac=Ek
因为到达c点时的小球的动能最大,所以Uac最大,即在圆周上找不到与c电势相等的点.且由a到c电场力对小球做正功.
过c点作切线,则cF为等势线.
过a点作cF的垂线,则该线为电场线,场强方向如图示.
∵∠cab=30°
∴连接co∠aco=30°
∵co∥am
∴电场方向与ac间的夹角θ为30°
(2)小球只受电场力,做类平抛运动.
水平方向上:x=Rcos30°=v0t
竖直方向上:y=R+Rsin30°=
由以上两式得:Ek=
mv2=
qER
因此初速度为v=
(3)根据题意可知,粒子做类平抛运动,由运动的合成与分解,在电场力的方向,在相同的电场力作用下,虽初动能相同,但因质量的不同,导致加速度的不一,由运动学公式s=
at2,可知,当加速度大的,要确保时间相同,则位移必须大,而加速度大的,质量偏小,则速度偏大,发生的垂直电场力方向的位移偏大,因此不可能同时落在同一圆周上,故没有其它粒子同时落到圆周上.
答:(1)电场的方向与AC间的夹角为30°;
(2)小球在A点的初速度与电场方向垂直,小球恰能落到C点,则初速度为
;
(3)没有同时落在圆周上的粒子.
因为到达c点时的小球的动能最大,所以Uac最大,即在圆周上找不到与c电势相等的点.且由a到c电场力对小球做正功.

过c点作切线,则cF为等势线.
过a点作cF的垂线,则该线为电场线,场强方向如图示.
∵∠cab=30°
∴连接co∠aco=30°
∵co∥am
∴电场方向与ac间的夹角θ为30°
(2)小球只受电场力,做类平抛运动.
水平方向上:x=Rcos30°=v0t
竖直方向上:y=R+Rsin30°=
| qEt2 |
| 2m |
由以上两式得:Ek=
| 1 |
| 2 |
| 1 |
| 8 |
因此初速度为v=
|
(3)根据题意可知,粒子做类平抛运动,由运动的合成与分解,在电场力的方向,在相同的电场力作用下,虽初动能相同,但因质量的不同,导致加速度的不一,由运动学公式s=
| 1 |
| 2 |
答:(1)电场的方向与AC间的夹角为30°;
(2)小球在A点的初速度与电场方向垂直,小球恰能落到C点,则初速度为
|
(3)没有同时落在圆周上的粒子.
点评:本题关键考查对电场力做功公式W=qEd的理解和应用,d是沿电场方向两点间的距离.此题要求熟练掌握功能关系和类平抛运动,属于难题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 如图所示,ab是半径为R的圆的一条直径,该圆处于匀强电场中,场强大小为E,方向一定.在圆周平面内,将一带正电q的小球从a点相同的动能抛出,抛出方向不同时小球会经过圆周上不同的点,在这些所有的点中,到达c点时的小球的动能最大,已知∠cab=30°,若不计重力和空气阻力,试求:
如图所示,ab是半径为R的圆的一条直径,该圆处于匀强电场中,场强大小为E,方向一定.在圆周平面内,将一带正电q的小球从a点相同的动能抛出,抛出方向不同时小球会经过圆周上不同的点,在这些所有的点中,到达c点时的小球的动能最大,已知∠cab=30°,若不计重力和空气阻力,试求: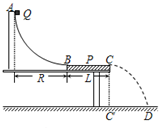 测量小物块Q与平板P之间的动摩擦因数的实验装置如图所示.AB是半径足够大的、光滑的四分之一圆弧轨道,与水平固定放置的P板的上表面BC在B点相切,C点在水平地面的垂直投影为C′.重力加速度为g.实验步骤如下:
测量小物块Q与平板P之间的动摩擦因数的实验装置如图所示.AB是半径足够大的、光滑的四分之一圆弧轨道,与水平固定放置的P板的上表面BC在B点相切,C点在水平地面的垂直投影为C′.重力加速度为g.实验步骤如下: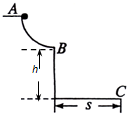 如图所示,AB是半径为R的
如图所示,AB是半径为R的 如图所示,AB是半径为R的1/4光滑圆弧轨道.B点是圆弧轨道的最低点,且过B点的切线在水平方向,B点离水平地面高h=R,有一质量为m的物体(可视为质点)从A点静止开始滑下,经过B点落到水平地面上.重力加速度为g.求:
如图所示,AB是半径为R的1/4光滑圆弧轨道.B点是圆弧轨道的最低点,且过B点的切线在水平方向,B点离水平地面高h=R,有一质量为m的物体(可视为质点)从A点静止开始滑下,经过B点落到水平地面上.重力加速度为g.求: