题目内容
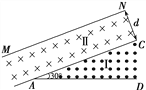
【题目】在方向水平、足够大的匀强电场中，一不可伸长的绝缘细线的一端连着一个质量为m、带电量为q的带电小球，另一端固定于O点，平衡时细线与竖直方向的夹角成30°:
（1）电场强度的大小；
（2）若剪断细线，则小球的加速度有多大；
（3）剪断细线开始经历1秒小球电势能的变化. (最后答案用m、q、g等符号表示)
【答案】（1）
（2）
（3）
【解析】
(1)受力分析结合，根据平衡条件即可求解；(2) 若剪断细线，先求合力在根据牛顿第二定律解题；(3)电场力所做的功等于电势能的变化量。
（1）带电小球在重力mg、电场力qE和绳的拉力T作用下处于平衡
则有：
解得：
（2）剪断细线时小球在重力mg、电场力qE 的合力作用下，沿细线方向做匀加速直线运动由牛顿第二定律得：
解得：
（3）1秒钟内小球发生的位移：
小球沿电场线移动的位移
所以电势能的变化
练习册系列答案
相关题目
