题目内容
15.如图所示,倾角θ=37°、高为h的斜面固定在水平地面上.小球从高为H(h<H<$\frac{13}{9}h$)处自由下落,总能与斜面上的特定小装置做无能量损失的碰撞后,水平抛出.小球自由下落到斜面上的落点距斜面左侧的水平距离x满足一定条件时,小球能直接落到水平地面.已知cos37°=$\frac{4}{5}$,sin37°=$\frac{3}{5}$,忽略空气阻力. (1)求小球落到水平地面时的速度大小.
(1)求小球落到水平地面时的速度大小.(2)要使小球做平抛运动后能直接落到水平地面,求x应满足的条件.
(3)在满足(2)的条件下,求小球运动最长时间.
分析 (1)由于小球与斜面碰撞无能量损失,自由下落和平抛运动机械能也守恒,所以小球整个运动过程中机械能守恒,据此列式求解小球落到地面上的速度大小;
(2)小球与斜面碰撞后做平抛运动,当正好落在斜面底端时,x最小,根据平抛运动的基本公式结合几何关系、动能定理求出x的最小值,而x的最大值即为h,从而求出x的范围;
(3)根据竖直方向做自由落体运动,由运动学公式列出总时间的表达式,再由数学知识求解最长的时间.
解答 解:(1)设小球落到水平地面时的速度为v,由机械能守恒得,
mgH=$\frac{1}{2}m{v}^{2}$,
解得v=$\sqrt{2gH}$.
(2)小球自由下落的落点距斜面左侧的水平距离x时,设小球做自由落体运动的末速度为v0,由运动学公式得,
${{v}_{0}}^{2}=2g(H-h+\frac{3}{4}x)$,
设小球做平抛运动落到水平地面所用的时间为t,由平抛运动规律得,
$h-\frac{3}{4}x=\frac{1}{2}g{t}^{2}$,
s=v0t,
联立解得s=$2\sqrt{(H-h+\frac{3}{4}x)(h-\frac{3}{4}x)}$.
由题意得,使小球做平抛运动后能直接落到水平地面,应有:
s$>\frac{4}{3}h-x$,
解得$\frac{4}{3}h>x>(\frac{4}{3}h-\frac{12}{13}H)$.
(3)小球自由下落的落点距斜面左侧的水平距离x时,设小球做自由落体所用时间为t0,由运动学公式得,
$(H-h+\frac{3}{4}x)=\frac{1}{2}g{{t}_{0}}^{2}$.
设小球由释放到落到水平地面运动的时间为t总,则
t总=t0+t,
解得${t}_{总}=\sqrt{\frac{2(H-h+\frac{3}{4}x)}{g}}+\sqrt{\frac{2(h-\frac{3}{4}x)}{g}}$,
整理得,${{t}_{总}}^{2}=\frac{2H}{g}+\frac{4\sqrt{(H-h+\frac{3}{4}x)(h-\frac{3}{4}x)}}{g}$,
由上式可知,当H-h+$\frac{3}{4}x$=h-$\frac{3}{4}x$,即x=$\frac{2}{3}(2h-H)$时,小球运动时间最长,设为tm,
则${t}_{m}=2\sqrt{\frac{H}{g}}$.
答:(1)小球落到水平地面时的速度大小为$\sqrt{2gh}$.
(2)x应满足的条件为$\frac{4}{3}h>x>(\frac{4}{3}h-\frac{12}{13}H)$.
(3)小球运动最长时间为$2\sqrt{\frac{H}{g}}$.
点评 本题是机械能守恒与自由落体运动、平抛运动的综合,既要把握每个过程的物理规律,更要抓住它们之间的联系,比如几何关系,运用数学上函数法求解极值.

 阅读快车系列答案
阅读快车系列答案 如图所示,在光滑水平面上停放着质量为m、装有光滑弧形槽的小车,一质量也为m的小球以水平初速度v0沿水平槽口向小车滑去,到达某一高度后,小球又返回左端,则( )
如图所示,在光滑水平面上停放着质量为m、装有光滑弧形槽的小车,一质量也为m的小球以水平初速度v0沿水平槽口向小车滑去,到达某一高度后,小球又返回左端,则( )| A. | 小球离开小车左端时将做自由落体运动 | |
| B. | 小球离开小车左端时将向右做平抛运动 | |
| C. | 整个过程小球和小车组成系统动量守恒 | |
| D. | 小球在弧形槽内上升的最大高度为$\frac{{{v}_{0}}^{2}}{2g}$ |
| A. | 该式适用于所有电场 | B. | 该式仅适用于匀强电场 | ||
| C. | 该式仅适用于点电荷形成的电场 | D. | 电场强度E的方向与F的方向相同 |
 如图所示,一木块在垂直于倾斜天花板平面方向上的推力F的作用下处于静止状态,则下列判断中正确的是( )
如图所示,一木块在垂直于倾斜天花板平面方向上的推力F的作用下处于静止状态,则下列判断中正确的是( )| A. | 天花板对木块的摩擦力可能为零 | |
| B. | 天花板与木块间的弹力一定不为零 | |
| C. | 木块所受天花板的摩擦力随推力F的增大而变化 | |
| D. | 在逐渐增大推力F的过程中,木块将始终保持静止 |
 粗糙水平面上,一个小球向右运动,将弹簧压缩,随后又被弹回直到离开弹簧.则该小球从接触到离开弹簧这个过程中,加速度大小的变化情况是( )
粗糙水平面上,一个小球向右运动,将弹簧压缩,随后又被弹回直到离开弹簧.则该小球从接触到离开弹簧这个过程中,加速度大小的变化情况是( )| A. | 先增大后减小 | B. | 先减小后增大 | ||
| C. | 先增大后减小再增大 | D. | 先减小后增大再减小 |
| A. | $\frac{m{v}^{2}}{GF}$ | B. | $\frac{m{v}^{4}}{GF}$ | C. | $\frac{2m{v}^{2}}{GF}$ | D. | $\frac{2m{v}^{4}}{GF}$ |
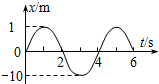
| A. | 振动图象从平衡位置开始计时 | B. | 2s末速度沿x轴负方向,加速度最大 | ||
| C. | 2s末速度最大,加速度为零 | D. | 1s末速度最大,加速度为零 |
 如图所示,无限大均匀带正电薄板竖直放置,其周围空间的电场可认为是匀强电场. 光滑绝缘细管垂直于板穿过中间小孔,细管内一个视为质点的带负电小球仅在电场力作用下运动,经过O点时速率为v0,动能为EK0.以小孔为原点建立x轴,规定x轴正方向为加速度a、速度v的正方向,薄板电势为+φ.下图分别表示x轴上各点的电势φ,小球的加速度a、速度v和动能Ek随x的变化图象,其中正确的是( )
如图所示,无限大均匀带正电薄板竖直放置,其周围空间的电场可认为是匀强电场. 光滑绝缘细管垂直于板穿过中间小孔,细管内一个视为质点的带负电小球仅在电场力作用下运动,经过O点时速率为v0,动能为EK0.以小孔为原点建立x轴,规定x轴正方向为加速度a、速度v的正方向,薄板电势为+φ.下图分别表示x轴上各点的电势φ,小球的加速度a、速度v和动能Ek随x的变化图象,其中正确的是( )


