题目内容
 在水平路面上用绳子拉一只质量为100kg的小车,绳子与路面的夹角θ=37°,拉力大小是200N,小车与地面间的动摩擦因数是0.1,小车由静止开始运动,已知g=10m/s2,sin37°=0.6,cos37°=0.8.求:
在水平路面上用绳子拉一只质量为100kg的小车,绳子与路面的夹角θ=37°,拉力大小是200N,小车与地面间的动摩擦因数是0.1,小车由静止开始运动,已知g=10m/s2,sin37°=0.6,cos37°=0.8.求:(1)小车的加速度是多大?
(2)小车5秒后的速度是多大?
(3)5秒末撤去拉力,小车通过的总位移是多大?
分析:(1)对小车进行受力分析,根据牛顿第二定律求解加速度;
(2)根据速度时间公式求出5秒后的速度;
(3)根据匀加速直线运动位移时间公式求出5s内的位移,5秒末撤去拉力,根据牛顿第二定律求出此时加速度,根据速度位移公式求出还能滑行的位移,
从而求出总位移.
(2)根据速度时间公式求出5秒后的速度;
(3)根据匀加速直线运动位移时间公式求出5s内的位移,5秒末撤去拉力,根据牛顿第二定律求出此时加速度,根据速度位移公式求出还能滑行的位移,
从而求出总位移.
解答:解:(1)设物体受支持力为FN,对物体受力分析,如图:
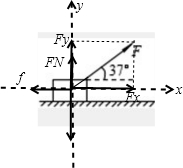
物小车竖直方向受力平衡:FN+Fsinθ=mg
解得:FN+=1000-200×0.6=880N;
水平方向根据牛顿第二定律得:Fcosθ-μFN=ma
解得:a=
=0.72m/s2;
(2)小车5秒后的速度v=at=5×0.72=3.6m/s;
(3)小车5秒内的位移x1=
at2=
×0.72×25=9m
撤去拉力后,根据牛顿第二定律得:a′=
=-0.1×10=-1m/s2
根据位移速度公式得:x2=
=
=6.48m;
所以小车运动的总位移x=x1+x2=9+6.48=15.48m;
答:(1)小车的加速度是0.72m/s2;
(2)小车5秒后的速度是3.6m/s;
(3)5秒末撤去拉力,小车通过的总位移是6.48m.

物小车竖直方向受力平衡:FN+Fsinθ=mg
解得:FN+=1000-200×0.6=880N;
水平方向根据牛顿第二定律得:Fcosθ-μFN=ma
解得:a=
| 200×0.8-0.1×880 |
| 100 |
(2)小车5秒后的速度v=at=5×0.72=3.6m/s;
(3)小车5秒内的位移x1=
| 1 |
| 2 |
| 1 |
| 2 |
撤去拉力后,根据牛顿第二定律得:a′=
| -μmg |
| m |
根据位移速度公式得:x2=
| v2-v02 |
| 2a′ |
| 0-3.62 |
| -2 |
所以小车运动的总位移x=x1+x2=9+6.48=15.48m;
答:(1)小车的加速度是0.72m/s2;
(2)小车5秒后的速度是3.6m/s;
(3)5秒末撤去拉力,小车通过的总位移是6.48m.
点评:本题关键是多次根据牛顿第二定律列式求解加速度,然后根据运动学公式列式求解运动学参量.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 在水平路面上用绳子拉一只重100N的箱子,绳子和路面的夹角为37°,如图所示.当绳子的拉力为50N,恰好使箱子匀速移动,求箱子和地面间的动摩擦因数.(g=10m/s2 sin37°=0.6)
在水平路面上用绳子拉一只重100N的箱子,绳子和路面的夹角为37°,如图所示.当绳子的拉力为50N,恰好使箱子匀速移动,求箱子和地面间的动摩擦因数.(g=10m/s2 sin37°=0.6) 在水平路面上用绳子拉一只重19kg的箱子,绳子和路面的夹角为37°,如图所示,当绳子的拉力为50N时,箱子恰好能够匀速移动,若g=10m/s2,求箱子和地面间的动摩擦因数是多少?(sin37°=0.6,cos37°=0.8)
在水平路面上用绳子拉一只重19kg的箱子,绳子和路面的夹角为37°,如图所示,当绳子的拉力为50N时,箱子恰好能够匀速移动,若g=10m/s2,求箱子和地面间的动摩擦因数是多少?(sin37°=0.6,cos37°=0.8)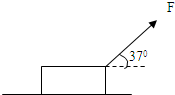 在水平路面上用绳子拉一只重100N的箱子做匀速直线运动,绳子拉力的大小为50N,方向与路面的夹角为37°,(已知sin37°=0.6,cos37°=0.8)问:
在水平路面上用绳子拉一只重100N的箱子做匀速直线运动,绳子拉力的大小为50N,方向与路面的夹角为37°,(已知sin37°=0.6,cos37°=0.8)问: