题目内容
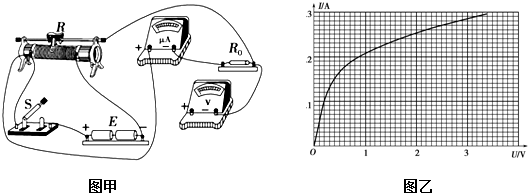
19.现要测量滑块与木板之间的动摩擦因数,实验装置如图1所示.表面粗糙的木板一端固定在水平桌面上,另一端抬起一定高度构成斜面;木板上有一滑块,其后端与穿过打点计时器的纸带相连,打点计时器固定在木板上,连接频率为50Hz的交流电源.接通电源后,从静止释放滑块,滑块带动纸带上打出一系列点迹.
(1)图2给出的是实验中获取的一条纸带的一部分:0、1、2、3、4、5、6是实验中选取的计数点,每相邻两计数点间还有4个打点(图中未标出),2、3和5、6计数点间的距离如图2所示.由图中数据求出滑块的加速度a=2.51m/s2(结果保留三位有效数字).
(2)已知木板的长度为L,为了求出滑块与木板间的动摩擦因数,还应测量的物理量是D.
| A.滑块到达斜面底端的速度v | B.滑块的质量m | C.滑块的运动时间t | D.斜面高度h和底边长度x |
分析 (1)利用逐差法△x=aT2可以求出物体的加速度大小,根据匀变速直线运动中某点的瞬时速度等于该过程中的平均速度大小可以求出某点的瞬时速度大小;
(2)根据牛顿第二定律有μmgcosθ=ma,由此可知需要测量的物理量.
(3)根据牛顿第二定律的表达式,可以求出摩擦系数的表达式
解答 解:(1)每相邻两计数点间还有4个打点,说明相邻的计数点时间间隔:T=0.1s,
x56=14.23cm=0.1423m,x23=6.70cm=0.0670m
根据逐差法有:a=$\frac{{x}_{56}-{x}_{23}}{3{T}^{2}}=\frac{0.1423-0.0670}{3×0.{1}^{2}}$m/s2=2.51m/s2;
(2)要测量动摩擦因数,由μmgcosθ=ma,可知要求μ,需要知道加速度与夹角余弦值,纸带数据可算出加速度大小,
再根据斜面高度h和底边长度x,结合三角知识,即可求解,故ABC错误,D正确.
(3)以滑块为研究对象,根据牛顿第二定律有:
mgsinθ-μmgcosθ=ma
解得:μ=$\frac{a+gsinθ}{gcosθ}$=$\frac{al+gh}{gx}$.
故答案为:(1)2.51;(2)D;(3)$\frac{al+gh}{gx}$
点评 解决实验问题首先要掌握该实验原理,了解实验的操作步骤和数据处理以及注意事项,同时要熟练应用所学基本规律解决实验问题

练习册系列答案
相关题目
9.如图所示,是A、B两质点运动的x-t图象,则下列说法不正确的是( )
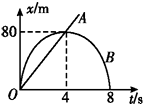

| A. | A质点以20 m/s的速度匀速运动 | |
| B. | B质点最初4 s做加速运动,后4 s做减速运动 | |
| C. | B质点先沿正方向做直线运动,后沿负方向做直线运动 | |
| D. | A、B两质点在4 s末相遇 |
10.下列关于加速度的说法,正确的是( )
| A. | 只要物体的速度不为零,加速度就不为零 | |
| B. | 只要物体的速度变化量大,加速度就大 | |
| C. | 只要物体的速度大,加速度就大 | |
| D. | 只要物体的速度变化率大,加速度就大 |
7.关于质点,下列说法正确的是( )
| A. | 研究地球自转时,可以把地球看成质点 | |
| B. | 测算火车从银川到北京的运行时间时,可以把火车看成质点 | |
| C. | 研究直升飞机螺旋桨的运动时,可以把螺旋桨看成质点 | |
| D. | 研究自行车车轮的转动时,可以把车轮看成质点 |
4.下列四组中皆为矢量的一组是( )
| A. | 位移、路程、加速度 | B. | 位移、速度的变化、加速度 | ||
| C. | 时刻、速度、加速度 | D. | 速度、时间、位移 |
8.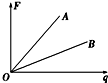 在某一电场中的A、B两处分别引入不同的试探电荷q,得到试探电荷所受的电场力随电荷量变化的关系如图示,则A、B两处电场强度EA、EB的大小关系是( )
在某一电场中的A、B两处分别引入不同的试探电荷q,得到试探电荷所受的电场力随电荷量变化的关系如图示,则A、B两处电场强度EA、EB的大小关系是( )
 在某一电场中的A、B两处分别引入不同的试探电荷q,得到试探电荷所受的电场力随电荷量变化的关系如图示,则A、B两处电场强度EA、EB的大小关系是( )
在某一电场中的A、B两处分别引入不同的试探电荷q,得到试探电荷所受的电场力随电荷量变化的关系如图示,则A、B两处电场强度EA、EB的大小关系是( )| A. | EA>EB | B. | EA<EB | ||
| C. | EA=EB | D. | 不能判定EA、EB的大小 |

 质量为m的物体,静止于一个倾角为α的斜面上,如图所示,如果已知物体所受重力和斜面对物体的弹力的合力方向平行于斜面向下,则这两个力的合力大小为mgsinα,斜面对物体的弹力大小为mgcosα,斜面对物体施加的摩擦力大小为mgsinα,方向平行于斜面向上.
质量为m的物体,静止于一个倾角为α的斜面上,如图所示,如果已知物体所受重力和斜面对物体的弹力的合力方向平行于斜面向下,则这两个力的合力大小为mgsinα,斜面对物体的弹力大小为mgcosα,斜面对物体施加的摩擦力大小为mgsinα,方向平行于斜面向上.