��Ŀ����
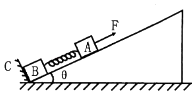
����Ŀ����ͼ��ʾ��MN��PQΪ���L=0.5m���㹻����ƽ�е��죬NQ��MN����ƽ����ˮƽ���ļнǦ�=37�㣬NQ������һ��R=4���ĵ��裮һ��ǿ�ų���ֱ�ڵ���ƽ�棬�Ÿ�Ӧǿ��B=1T����һ������m=0.05kg������R=1���Ľ�����ab������NQ�����ڵ����ϣ����뵼��Ӵ����ã�����ĵ��費�ƣ��־�ֹ�ͷŽ��������������ص��������˶�������ʼ����NQƽ�У���֪�������뵼���Ķ�Ħ��������=0.5����������������cd��ʱ�Ѿ��ﵽ�ȶ��ٶȣ���gȡl0m/s2 �� sin37��=0.6��cos37��=0.8�����ʣ�
��1����������������cd��ʱ��·�еĵ������
��2���������ﵽ���ȶ�ʱ���ٶȶ��
���𰸡�
��1���⣺���������ﵽ�ȶ��ٶ�ʱ��
��ƽ�������ã�mgsin��=f+F
mgcos��=N
��f=��N
�������ݿɵã�F=0.1N
����F=BIL���ɵ�
![]() =
= ![]()
��2���⣺�ɸ�Ӧ�綯��E=BLv��I= ![]() �õ�
�õ�
v= ![]() �������ݿɵã�v=2m/s
�������ݿɵã�v=2m/s
����������1�����⣬��������������cd��ʱ�Ѿ��ﵽ�ȶ��ٶȣ���ʱ��������ʼ������ֱ���˶�������ƽ��״̬������ƽ������������������ɰ�������ʽ�����������2���ɱպϵ�·ŷķ���������Ӧ�綯�ƣ�������ٶȣ�