题目内容
【题目】如图所示,一传送带与水平面的夹角=30°,且以v1=2m/s的速度沿顺时针方向传动。一质量m=1kg的小物块以v2=4m/s的速度滑上传送带的底端,最终又从传送带的底端滑出。已知小物块与传送带间的动摩擦因数=![]() ,传送带足够长,重力加速度g=10m/s2。求:(
,传送带足够长,重力加速度g=10m/s2。求:(![]() )
)
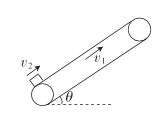
(1)小物块沿传送带向上滑行的时间t;
(2)小物块离开传送带时的速度大小v;
(3)小物块在传送带上运动随个过程中,小物块与传送带间因摩擦产生的内能E。
【答案】(1)1.25s(2)2.6m/s(3)16.8J
【解析】(1)由题可知,小物块在开始时受到传送带的滑动摩擦力沿传送带向下,设其做匀减速运动的加速度大小为1,有:mgsin+mgcos=m1
解得1=8m/s2
其速度减小到v1=2m/s所用的时间:t1=![]() =0.25s
=0.25s
之后,小物块受到传送带的滑动摩擦力沿传送带向上,设其加速度大小为2,有:
mgsin-mgcos=m2
解得:2=2m/s2
小物块减速到0所用的时间:t2=![]() =1s
=1s
又t=t1+t2
解得:t=1.25s
(2)小物块沿传送带向上滑行的最大距离为: ![]() (1分)
(1分)
解得:x=1.75m(1分)
又由于物块沿传送带下滑时,受到的滑动摩擦力沿传送带向上,其加速度大小仍为2=2m/s2,有:2a2x=v2
解得:v=![]() m/s=2.6m/s
m/s=2.6m/s
(3)小物块向上减速的第一阶段,相对位移大小: ![]()
小物块向上减速的第二阶段,相对位移大小: ![]()
小物块向下加速阶段,相对位移大小: ![]()
![]()
解得: ![]()
故所求内能: ![]()

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目