题目内容
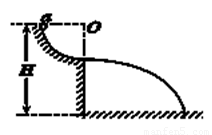
 如图所示,有一光滑的直角支架MON直立在水平地面上,支架的竖直部分OM长为2l.两个质量均为m的小球A和B套在支架上,并通过长为l的细绳相连.现从图示位置(细绳与竖直方向的夹角θ=60°)由静止开始释放两球,当小球B运动到支架O处时,与放在该处的小球C(图中未画出)发生碰撞,碰后小球B静止,而小球C水平抛出,落地时,落点到M的距离为l.试求:
如图所示,有一光滑的直角支架MON直立在水平地面上,支架的竖直部分OM长为2l.两个质量均为m的小球A和B套在支架上,并通过长为l的细绳相连.现从图示位置(细绳与竖直方向的夹角θ=60°)由静止开始释放两球,当小球B运动到支架O处时,与放在该处的小球C(图中未画出)发生碰撞,碰后小球B静止,而小球C水平抛出,落地时,落点到M的距离为l.试求:(1)小球B所能达到的最大速度;
(2)小球C的质量.
分析:(1)小球B在拉力作用下一直做加速运动,当运动到O点时速度最大,对A、B组成的系统研究,根据机械能守恒定律求出小球B所能达到的最大速度.
(2)根据平抛运动的规律求出小球C碰后的速度,对B和C组成的系统研究,根据动量守恒定律求出小球C的质量.
(2)根据平抛运动的规律求出小球C碰后的速度,对B和C组成的系统研究,根据动量守恒定律求出小球C的质量.
解答:解:(1)两球释放后,小球B在细绳拉力作用下一直向右加速,当小球B运动到支架O处时速度达到最大,设为vB,而此时小球A不再向下运动,速度刚好为0,根据机械能守恒定律有
mg l(1-cos60°)=
mvB2
解得 vB=
(2)设小球C的质量为mC,碰后小球C的速度为vC,根据平抛运动规律有
2l=
gt2
l=vCt
解得 vC=
碰撞时,小球B、C组成的系统动量守恒,根据动量守恒定律有
mvB=mCvC
解得 mC=2m
答:(1)小球B所能达到的最大速度为
.
(2)小球C的质量为2m.
mg l(1-cos60°)=
| 1 |
| 2 |
解得 vB=
| gl |
(2)设小球C的质量为mC,碰后小球C的速度为vC,根据平抛运动规律有
2l=
| 1 |
| 2 |
l=vCt
解得 vC=
| 1 |
| 2 |
| gl |
碰撞时,小球B、C组成的系统动量守恒,根据动量守恒定律有
mvB=mCvC
解得 mC=2m
答:(1)小球B所能达到的最大速度为
| gl |
(2)小球C的质量为2m.
点评:本题综合考查了动量守恒定律和机械能守恒定律,综合性较强,知道小球B运动到0点时速度最大.

练习册系列答案
相关题目
 (2010?镇江一模)如图所示,有一光滑的半径可变的
(2010?镇江一模)如图所示,有一光滑的半径可变的 如图所示,有一光滑的T字形支架,在它的竖直杆上套有一个质量为m1的物体A,用长为l的不可伸长的细绳悬挂在套于水平杆上的小环B下,B的质量为m2=m1=m开始时A处于静止状态,系绳处于竖直状态.今用水平恒力F=3mg拉小环B,使A上升至细绳与水平杆成37°,
如图所示,有一光滑的T字形支架,在它的竖直杆上套有一个质量为m1的物体A,用长为l的不可伸长的细绳悬挂在套于水平杆上的小环B下,B的质量为m2=m1=m开始时A处于静止状态,系绳处于竖直状态.今用水平恒力F=3mg拉小环B,使A上升至细绳与水平杆成37°,