题目内容
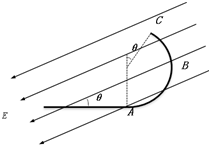
2006年都灵冬奥会上,我国选手以总分250.77的成绩创造中国自由式滑雪的里程碑,实现了我国冬奥史上金牌两个“零的突破”(男子项目金牌零的突破和雪上项目金牌零的突破),创造了我国冬奥会历史上的奇迹.自由式滑雪的运动模型可简化如下:如图所示,斜面轨道AB与水平面之间的夹角θ=53°,BD为半径R=4m的圆弧形轨道,且B点与D点在同一水平面上,在B点,轨道AB与圆弧形轨道BD相切,整个轨道处于竖直平面内且处处光滑,在A点处的一质量m=1kg的小球由静止滑下,经过B、C点后从D点斜抛出去,最后落在地面上的S点处时的速度大小vs=8m/s,已知A点距地面的高度H=10m,B点距地面的高度h=5m,设以MDN为分界线,假设其左边为存在空气阻力的区域,右边为不考虑空气阻力的真空区域,g取10m/s2,cos53°=0.6
(1)小球经过B点的速度为多大?
(2)小球经过圆弧轨道最低处C点时对轨道的压力多大?
(3)小球从D点抛出后,在MDN分界线左边的区域受到的阻力f与其瞬时速度方向始终相反,求小球从D点至S点的过程中,阻力f所做的功.

(1)小球经过B点的速度为多大?
(2)小球经过圆弧轨道最低处C点时对轨道的压力多大?
(3)小球从D点抛出后,在MDN分界线左边的区域受到的阻力f与其瞬时速度方向始终相反,求小球从D点至S点的过程中,阻力f所做的功.

(1)从A到B过程中,由动能定理得:
mg(H-h)=
mvB2-0,
解得:vB=
=10m/s;
(2)由数学知识可知,OB与OC间的夹角是53°,
hBC=R-Rcos53°=1.6m,
由A到C过程中,由动能定理可得:
mg(H-h)+mghBC=
mvC2-0,
小球做圆周运动,由牛顿第二定律得:
F-mg=
,解得:F=43N;
由牛顿第三定律得,小球对轨道的压力F′=F=43N;
(3)B点与D点在同一水平面上,vD=vB=10m/s,
从D到S过程中,阻力做负功,由动能定理可得:
mgh-Wf=
mvS2-
mvD2,解得:Wf=68J;
答:(1)小球经过B点的速度为10m/s.
(2)小球经过圆弧轨道最低处C点时对轨道的压力为43N.
(3)阻力f所做的功为-68J.
mg(H-h)=
| 1 |
| 2 |
解得:vB=
| 2(H-h)g |
(2)由数学知识可知,OB与OC间的夹角是53°,
hBC=R-Rcos53°=1.6m,
由A到C过程中,由动能定理可得:
mg(H-h)+mghBC=
| 1 |
| 2 |
小球做圆周运动,由牛顿第二定律得:
F-mg=
m
| ||
| R |
由牛顿第三定律得,小球对轨道的压力F′=F=43N;
(3)B点与D点在同一水平面上,vD=vB=10m/s,
从D到S过程中,阻力做负功,由动能定理可得:
mgh-Wf=
| 1 |
| 2 |
| 1 |
| 2 |
答:(1)小球经过B点的速度为10m/s.
(2)小球经过圆弧轨道最低处C点时对轨道的压力为43N.
(3)阻力f所做的功为-68J.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目