题目内容
有一带负电的小球,其带电量q=—2×10-3C。如图所示,开始时静止在场强E="200" N/C的匀强电场中的P点,靠近电场极板B有一挡板S,小球与挡板S的距离h=5cm,与A板距离H="45" cm,重力作用不计。在电场力作用下小球向左运动,与挡板S相碰后电量减少到碰前的k倍,已知k=5/6 ,而碰后小球的速度大小不变.

(1)设匀强电场中挡板S所在位置处电势为零,则电场中P点的电势为多少?小球在P点时的电势能为多少?(电势能用Ep表示)
(2)小球从P点出发第一次回到最右端的过程中电场力对小球做了多少功?
(3)小球经过多少次碰撞后,才能抵达A板?(取lg1.2=0.08)

(1)设匀强电场中挡板S所在位置处电势为零,则电场中P点的电势为多少?小球在P点时的电势能为多少?(电势能用Ep表示)
(2)小球从P点出发第一次回到最右端的过程中电场力对小球做了多少功?
(3)小球经过多少次碰撞后,才能抵达A板?(取lg1.2=0.08)
(1) 0.02 J(2) 0(3) n≥12.5,即小球经过13次碰撞后,才能抵达A板
(1)由匀强电场的场强和电势差之间的关系式得USP=Eh
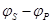 由电势差和电势之间的关系得USP=
由电势差和电势之间的关系得USP=
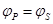 联立解得P点的电势为? -Eh="0" V -200×5×10-2 V="-10" V
联立解得P点的电势为? -Eh="0" V -200×5×10-2 V="-10" V
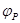 小球在P点的电势能为Ep=q =-2×10-3×(-10) J="0.02" J
小球在P点的电势能为Ep=q =-2×10-3×(-10) J="0.02" J
(2)对小球从P点出发第一次回到最右端的过程应用动能定理得W电=Ek1-Ek0
由题可知小球从P出发第一次回到最右端时速度为零,所以W电=Ek1-Ek0=0-0=0
(3)设碰撞n次后小球到达A板,对小球运动的全过程应用动能定理得
qEh-knqE(h+H)=Ekn-Ek0
小球到达A板的条件是:Ekn≥0
联立解得n≥12.5,即小球经过13次碰撞后,才能抵达A板
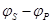 由电势差和电势之间的关系得USP=
由电势差和电势之间的关系得USP=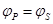 联立解得P点的电势为? -Eh="0" V -200×5×10-2 V="-10" V
联立解得P点的电势为? -Eh="0" V -200×5×10-2 V="-10" V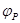 小球在P点的电势能为Ep=q =-2×10-3×(-10) J="0.02" J
小球在P点的电势能为Ep=q =-2×10-3×(-10) J="0.02" J(2)对小球从P点出发第一次回到最右端的过程应用动能定理得W电=Ek1-Ek0
由题可知小球从P出发第一次回到最右端时速度为零,所以W电=Ek1-Ek0=0-0=0
(3)设碰撞n次后小球到达A板,对小球运动的全过程应用动能定理得
qEh-knqE(h+H)=Ekn-Ek0
小球到达A板的条件是:Ekn≥0
联立解得n≥12.5,即小球经过13次碰撞后,才能抵达A板

练习册系列答案
相关题目
 ,设
,设 =k,则k的值可能为( )
=k,则k的值可能为( ) B
B  C
C  D
D 



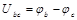 ,线框在图示位置的时刻作为时间的零点,则bc两点间的电势差随时间变化的图线应为
,线框在图示位置的时刻作为时间的零点,则bc两点间的电势差随时间变化的图线应为
 形盒
形盒 ,
, 构成,其间留有的窄缝处加有高频交变电压
构成,其间留有的窄缝处加有高频交变电压 (加速电压)
(加速电压)