题目内容
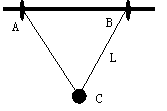
 在水平光滑细杆上穿着A、B两个小球(可看作质点),用两根长度同为L的不可伸长的轻绳与C球连接,如图所示.已知A、B、C三球质量均相同,开始时三球均静止;两绳伸直且处于水平状态.现同时释放三球.求:
在水平光滑细杆上穿着A、B两个小球(可看作质点),用两根长度同为L的不可伸长的轻绳与C球连接,如图所示.已知A、B、C三球质量均相同,开始时三球均静止;两绳伸直且处于水平状态.现同时释放三球.求:(1)从开始释放到三个小球完全静止,系统损失了多少机械能.
(2)释放过程中,在C球第一次运动到最低点.A、B两球刚要相碰的瞬间,A、B两球速度的大小.
分析:当小球C落到最低点时,A、B只有水平方向速度,根据系统水平方向动量守恒和系统机械能守恒可正确解答.
解答:解(1)从开始释放到三个小球完全静止,动能变化为零,小球C的机械能减小mgL
所以系统损失机械能是mgL
(2)设球的质量均为m,C球运动到最低点时A、B、C三球的速度分别为vA、vB、vC
则vC=0 ①
由系统水平方向的动量守恒得mvA-mvB=0 vA=vB ②
由A、B、C为系统,由机械能守恒定律:mgL=
mvA2+
mvB2③
由①②③式可得:vA=vB=
答:(1)从开始释放到三个小球完全静止,系统损失机械能是mgL.
(2)释放过程中,在C球第一次运动到最低点.A、B两球刚要相碰的瞬间,A、B两球速度的大小是
.
所以系统损失机械能是mgL
(2)设球的质量均为m,C球运动到最低点时A、B、C三球的速度分别为vA、vB、vC
则vC=0 ①
由系统水平方向的动量守恒得mvA-mvB=0 vA=vB ②
由A、B、C为系统,由机械能守恒定律:mgL=
| 1 |
| 2 |
| 1 |
| 2 |
由①②③式可得:vA=vB=
| gL |
答:(1)从开始释放到三个小球完全静止,系统损失机械能是mgL.
(2)释放过程中,在C球第一次运动到最低点.A、B两球刚要相碰的瞬间,A、B两球速度的大小是
| gL |
点评:正确应用某一方向上动量守恒和功能关系解题,平时要加强训练提高综合应用物理知识的能力.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 在水平光滑细杆上穿着A、B两个刚性小球(可看作质点),用两根长度同为L的不可伸长的轻绳与C球连接,如图所示.已知A、B、C三球质量均相同,开始时三球均静止、两绳伸直且处于水平状态.现同时释放三球,求:
在水平光滑细杆上穿着A、B两个刚性小球(可看作质点),用两根长度同为L的不可伸长的轻绳与C球连接,如图所示.已知A、B、C三球质量均相同,开始时三球均静止、两绳伸直且处于水平状态.现同时释放三球,求: