题目内容
【题目】如图所示,横梁BC为水平轻杆,且B端用铰链固定在竖直墙上,轻绳AD拴接在C端,D端所挂物体质量M=1kg,g取10m/s2 , 求: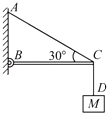
(1)轻绳AC的拉力FAC的大小;
(2)轻杆BC对C端的支持力.
【答案】
(1)
解:物体M处于平衡状态,与物体相连的轻绳拉力大小等于物体的重力,取C点为研究对象,进行受力分析,如图所示.
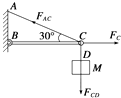
由平衡条件有:
FACsin 30°=FCD=Mg
可得 FAC=2Mg=2×10×10 N=20 N
(2)
解:由平衡方程得:
FACcos 30°﹣FC=0
得:FC=2Mgcos 30°= ![]() Mg≈17.3 N
Mg≈17.3 N
方向水平向右
【解析】物体处于平衡状态,与物体相连的轻绳拉力大小等于物体的重力,取C点为研究对象,进行受力分析,根据共点力平衡条件列式求解.
【考点精析】本题主要考查了力的分解的相关知识点,需要掌握求一个已知力的分力,叫做力的分解(力的分解与力的合成互为逆运算);在实际问题中,通常将已知力按力产生的实际作用效果分解;为方便某些问题的研究,在很多问题中都采用正交分解法才能正确解答此题.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案【题目】某同学在“用打点计时器测速度”的实验中,用打点计时器记录了被小车拖动的纸带的运动情况,在纸带上确定出A、B、C、D、E、F、G共7个计数点.其相邻点间的距离如图1所示,每两个相邻的测量点之间的时间间隔为0.10s.
(1)试根据纸带上各个计数点间的距离,每个0.10s测一次速度,计算出打下B、C、D、E、F五个点时小车的瞬时速度,并将各个速度值填入下表(要求保留3位有效数字)
vB | vC | vD | vE | vF | |
数值(m/s) |
(2)将B C D E F各个时刻的瞬时速度标在直角坐标系中,并在图2中画出小车的瞬时速度随时间变化的关系图线. 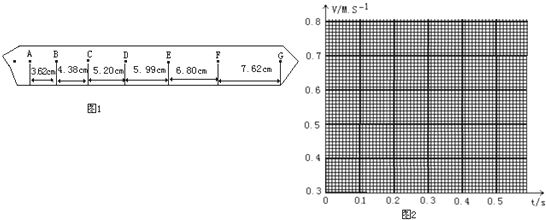
(3)由v﹣t图象可知打下A点时小车的瞬时速度vA= , 打下G点时小车的瞬时速度vB= .