题目内容
10.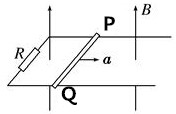 如图所示,一对光滑的平行金属导轨固定在同一水平面内,导轨的间距l=0.4m,在导轨的左端接有阻值R=0.2Ω的电阻,一质量m=0.1kg、电阻r=0.1Ω的金属棒PQ垂直于导轨放置其上,整个装置竖直向上、磁感应强度B=0.4T的匀强磁场中.现对金属棒施加一在水平向右的作用力,使其由静止开始以a=2m/s2的加速度做匀加速直线运动,在金属棒的位移x=9m时撤去外力,金属棒继续运动一段距离后停下来.已知导轨足够长且电阻不计,金属棒在运动过程中始终与导轨保持良好接触.撤去外力后,求:
如图所示,一对光滑的平行金属导轨固定在同一水平面内,导轨的间距l=0.4m,在导轨的左端接有阻值R=0.2Ω的电阻,一质量m=0.1kg、电阻r=0.1Ω的金属棒PQ垂直于导轨放置其上,整个装置竖直向上、磁感应强度B=0.4T的匀强磁场中.现对金属棒施加一在水平向右的作用力,使其由静止开始以a=2m/s2的加速度做匀加速直线运动,在金属棒的位移x=9m时撤去外力,金属棒继续运动一段距离后停下来.已知导轨足够长且电阻不计,金属棒在运动过程中始终与导轨保持良好接触.撤去外力后,求:(1)电阻R中产生的焦耳热QR;
(2)金属棒沿导线滑行的距离L(保留3位有效数字).
分析 (1)根据运动学公式求出撤去外力时金属棒的速度,撤去外力后棒在安培力作用下做减速运动,安培力做负功,使棒的动能转化为电能,再通过电流做功将电能转化为内能,产生的焦耳热等于棒的动能减少,求出撤去外力后R产生的焦耳热,从而得到总的焦耳热.
(3)对于匀加速运动过程,由运动学公式求出金属棒运动的距离.撤去外力后,根据牛顿第二定律和加速度的定义式,结合微元法求解滑行距离.再得到总距离L.
解答 解:(1)设撤去外力棒的速度为v.则有:
v=$\sqrt{2ax}$=$\sqrt{2×2×9}$=6m/s
撤去外力后棒在安培力作用下做减速运动,安培力做负功先将棒的动能转化为内能,所以回路中产生的焦耳热等于棒的动能减少.
由能量守恒定律得回路产生的总焦耳热为:Q总=△EK=$\frac{1}{2}$mv2=$\frac{1}{2}×0.1×{6}^{2}$=1.8J
则电阻R中产生的焦耳热为:QR=$\frac{R}{R+r}$总=$\frac{0.2}{0.2+0.1}$×1.8J=1.2J
(2)撤去外力后,设棒的速度为v时加速度大小为a.在极短时间△t内速度的变化量为△v,通过的位移为△x.
则有:a=$\frac{△v}{△t}$
取向右为正方向,根据牛顿第二定律得:-BIl=ma
又 I=$\frac{Blv}{R+r}$
联立得:-$\frac{{B}^{2}{l}^{2}v}{R+r}$=m$\frac{△v}{△t}$
则得:-$\frac{{B}^{2}{l}^{2}v}{R+r}$△t=m△v
两边求和得:$\sum_{\;}^{\;}$(-$\frac{{B}^{2}{l}^{2}v}{R+r}$△t)=$\sum_{\;}^{\;}$m△v
又△x=v△t
可得-$\frac{{B}^{2}{l}^{2}}{R+r}L$=0-mv
得 L=$\frac{mv(R+r)}{{B}^{2}{l}^{2}}$=$\frac{0.1×6×0.3}{0.{4}^{2}×0.{4}^{2}}$≈7.03m
答:
(1)电阻R中产生的焦耳热QR是1.2J
(2)金属棒沿导线滑行的距离L是7.03m.
点评 解决该题关键要会微元法求金属棒通过的距离,其切入口是牛顿第二定律和瞬时加速度的表达式,还要分析清楚运动过程中不同形式的能量中如何转化,运用能量守恒求热量.


| A. | 甲图表示电梯可能做匀速上升运动 | |
| B. | 乙图表示电梯可能做匀加速上升运动 | |
| C. | 丙图表示电梯可能做匀减速下降运动 | |
| D. | 丁图表示电梯可能做变减速下降运动 |
| A. | 自开始计时起,1s末的速度是7m/s | |
| B. | 这段运动所用时间是4s | |
| C. | 这段运动的加速度是1m/s2 | |
| D. | 从开始计时起,经过14m处的速度是5$\sqrt{2}$ m/s |
| A. | 因为工件在运动,所以甲、乙两种情况工件都受到与运动方向相反的摩擦力 | |
| B. | 因为工件在运动,所以甲、乙两种情况工件都受到与运动方向相同的摩擦力 | |
| C. | 因为甲情况工件与传送带之间不存在相对运动趋势,所以工件不受摩擦力作用 | |
| D. | 因为乙情况工件有沿传送带下滑的相对运动趋势,所以工件受沿倾斜面向上的静摩擦力作用 |
| A. | 物体的动能增加$\frac{mgh}{2}$ | B. | 物体的重力势能减少了$\frac{mgh}{2}$ | ||
| C. | 阻力做的功为$\frac{mgh}{2}$ | D. | 物体的机械能减少了mgh |
| A. | 第2s初 | B. | 从学校回家用了10分钟 | ||
| C. | 第1s内 | D. | 一节课45分钟 |
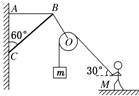 如图所示,轻质BC的C点用光滑铰链与墙壁固定,杆的B点通过水平细绳AB使杆与竖直墙壁保持60°的夹角.若在B点用细绳悬挂一个定滑轮(不计重力),某人用它匀速地提起重物.已知重物的质量m=30kg,人的质量M=50kg,连接人的绳子与水平方向的夹角始终保持30°,g取10m/s2.试求:(结果可以用根号表示)
如图所示,轻质BC的C点用光滑铰链与墙壁固定,杆的B点通过水平细绳AB使杆与竖直墙壁保持60°的夹角.若在B点用细绳悬挂一个定滑轮(不计重力),某人用它匀速地提起重物.已知重物的质量m=30kg,人的质量M=50kg,连接人的绳子与水平方向的夹角始终保持30°,g取10m/s2.试求:(结果可以用根号表示)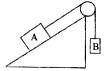 如图所示,A物体质量为2kg,斜面倾角为60°,木块A与斜面间的摩擦因数为0.1,则物体B的质量为多少时,木块能作匀速运动?
如图所示,A物体质量为2kg,斜面倾角为60°,木块A与斜面间的摩擦因数为0.1,则物体B的质量为多少时,木块能作匀速运动?