题目内容
10.质量为m的物体,在距地面h高处以$\frac{g}{2}$的加速度由静止开始竖直落下至地面,则下落过程中( )| A. | 物体的动能增加$\frac{mgh}{2}$ | B. | 物体的重力势能减少了$\frac{mgh}{2}$ | ||
| C. | 阻力做的功为$\frac{mgh}{2}$ | D. | 物体的机械能减少了mgh |
分析 通过动能定理求出动能的增加量.根据下落的高度求出重力势能的减小量.根据牛顿第二定律求出阻力,再求阻力做功.根据阻力做功情况确定机械能的变化量.
解答 解:A、根据牛顿第二定律得,小球所受的合力为:F合=ma=$\frac{1}{2}$mg,根据动能定理知:F合h=△Ek,则动能增加量为△Ek=$\frac{1}{2}$mgh.故A正确.
B、物体下降的高度是h,所以重力做功mgh,物体的重力势能减少mgh.故B错误.
C、阻力大小为F.根据牛顿第二定律得:mg-F=ma,解得:F=$\frac{1}{2}$mg,则阻力做功为-Fh=-$\frac{1}{2}$mgh.故C错误.
D、根据除重力以外其它力做功等于机械能的增量,知物体克服阻力做功为$\frac{1}{2}$mgh,所以机械能减少了$\frac{1}{2}$mgh.故D错误.
故选:A
点评 解决本题的关键掌握常见的功与能关系,知道合力做功等于动能的变化量,重力做功等于重力势能的减小量,除重力以外其它力做功等于机械能的增量.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.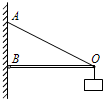 城市中的路灯、无轨电车的供电线路等,经常用三角形的结构悬挂.图是这类结构的一种简化模型,硬杆左端可绕通过B点且垂直于纸面的轴无摩擦的转动,右端O点通过钢索挂于A点,钢索和硬杆所受的重力均可忽略.有一质量不变的重物悬挂于O点,现将钢索缓慢变短,并使钢索的悬挂点A缓慢向下移动,以保证硬杆始终处于水平.则在上述变化过程中,下列说法中正确的是( )
城市中的路灯、无轨电车的供电线路等,经常用三角形的结构悬挂.图是这类结构的一种简化模型,硬杆左端可绕通过B点且垂直于纸面的轴无摩擦的转动,右端O点通过钢索挂于A点,钢索和硬杆所受的重力均可忽略.有一质量不变的重物悬挂于O点,现将钢索缓慢变短,并使钢索的悬挂点A缓慢向下移动,以保证硬杆始终处于水平.则在上述变化过程中,下列说法中正确的是( )
 城市中的路灯、无轨电车的供电线路等,经常用三角形的结构悬挂.图是这类结构的一种简化模型,硬杆左端可绕通过B点且垂直于纸面的轴无摩擦的转动,右端O点通过钢索挂于A点,钢索和硬杆所受的重力均可忽略.有一质量不变的重物悬挂于O点,现将钢索缓慢变短,并使钢索的悬挂点A缓慢向下移动,以保证硬杆始终处于水平.则在上述变化过程中,下列说法中正确的是( )
城市中的路灯、无轨电车的供电线路等,经常用三角形的结构悬挂.图是这类结构的一种简化模型,硬杆左端可绕通过B点且垂直于纸面的轴无摩擦的转动,右端O点通过钢索挂于A点,钢索和硬杆所受的重力均可忽略.有一质量不变的重物悬挂于O点,现将钢索缓慢变短,并使钢索的悬挂点A缓慢向下移动,以保证硬杆始终处于水平.则在上述变化过程中,下列说法中正确的是( )| A. | 硬杆对O点的弹力不变 | |
| B. | 钢索对O点的拉力变小 | |
| C. | 钢索和硬杆对O点的作用力的合力变大 | |
| D. | 钢索和硬杆对O点的作用力的合力不变 |
15.在用DIS实验研究小车加速度与外力的关系时,某实验小组先用如图(a)所示的实验装置,重物通过滑轮用细线拉小车,位移传感器(发射器)随小车一起沿倾斜轨道运动,位移传感器(接收器)固定在轨道一端.实验中把重物的重力作为拉力F,改变重物重力重复实验四次,列表记录四组数据.

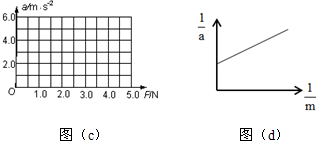
(1)在图(c)坐标纸上作出小车加速度a和拉力F的关系图线;
(2)从所得图线分析该实验小组在操作过程中的不当之处是倾角过大或平衡摩擦力过度;
(3)如果实验时,在小车和重物之间接一个不计质量的微型力传感器来测量绳子的拉力大小,如图(b)所示.要满足小车质量M远大于重物的质量m是不必要的.(填“必要”或“不必要”)
(4)如果实验装置如图(a),图为质量一定时,根据实验数据描绘的小车加速度a与重物的总质量m之间的关系图象.设图(d)中直线斜率为k,在纵轴上的斜率为b,若牛顿第二定律成立,则小车的重量G为$\frac{k}{{b}^{2}}$;当地的重力加速度为$\frac{1}{b}$.

(1)在图(c)坐标纸上作出小车加速度a和拉力F的关系图线;
(2)从所得图线分析该实验小组在操作过程中的不当之处是倾角过大或平衡摩擦力过度;
(3)如果实验时,在小车和重物之间接一个不计质量的微型力传感器来测量绳子的拉力大小,如图(b)所示.要满足小车质量M远大于重物的质量m是不必要的.(填“必要”或“不必要”)
| a/ms-2 | 2.01 | 2.98 | 4.02 | 6.00 |
| F/N | 1.00 | 2.00 | 3.00 | 5.00 |

2. 质量为m=2kg的物体沿水平面向右做直线运动,t=0时刻受到一个水平向左的恒力F,如图甲所示,此后物体的v-t图象如图乙所示,取水平向右为正方向,g=10m/s2,则( )
质量为m=2kg的物体沿水平面向右做直线运动,t=0时刻受到一个水平向左的恒力F,如图甲所示,此后物体的v-t图象如图乙所示,取水平向右为正方向,g=10m/s2,则( )
 质量为m=2kg的物体沿水平面向右做直线运动,t=0时刻受到一个水平向左的恒力F,如图甲所示,此后物体的v-t图象如图乙所示,取水平向右为正方向,g=10m/s2,则( )
质量为m=2kg的物体沿水平面向右做直线运动,t=0时刻受到一个水平向左的恒力F,如图甲所示,此后物体的v-t图象如图乙所示,取水平向右为正方向,g=10m/s2,则( )| A. | 物体与水平面间的动摩擦因数为μ=0.5 | |
| B. | 10s末恒力F的功率为6W | |
| C. | 10s末物体恰好回到计时起点位置 | |
| D. | 10s内物体克服摩擦力做功34J |
19.在2008年北京奥运会上,牙买加选手博尔特是公认的世界飞人,在男子100m决赛和男子200m决赛中分别以9.69s和19.30s的成绩打破两项世界纪录,获得两枚金牌.关于他在这两次决赛中的运动情况,下列说法中不正确的是( )
| A. | 200m决赛的平均速率约为10.36m/s | |
| B. | 200m决赛的位移是100 m决赛的两倍 | |
| C. | 100m决赛的平均速度约为10.32m/s | |
| D. | 100m决赛的最大速度由题目数据无法求出 |
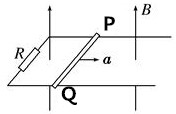 如图所示,一对光滑的平行金属导轨固定在同一水平面内,导轨的间距l=0.4m,在导轨的左端接有阻值R=0.2Ω的电阻,一质量m=0.1kg、电阻r=0.1Ω的金属棒PQ垂直于导轨放置其上,整个装置竖直向上、磁感应强度B=0.4T的匀强磁场中.现对金属棒施加一在水平向右的作用力,使其由静止开始以a=2m/s2的加速度做匀加速直线运动,在金属棒的位移x=9m时撤去外力,金属棒继续运动一段距离后停下来.已知导轨足够长且电阻不计,金属棒在运动过程中始终与导轨保持良好接触.撤去外力后,求:
如图所示,一对光滑的平行金属导轨固定在同一水平面内,导轨的间距l=0.4m,在导轨的左端接有阻值R=0.2Ω的电阻,一质量m=0.1kg、电阻r=0.1Ω的金属棒PQ垂直于导轨放置其上,整个装置竖直向上、磁感应强度B=0.4T的匀强磁场中.现对金属棒施加一在水平向右的作用力,使其由静止开始以a=2m/s2的加速度做匀加速直线运动,在金属棒的位移x=9m时撤去外力,金属棒继续运动一段距离后停下来.已知导轨足够长且电阻不计,金属棒在运动过程中始终与导轨保持良好接触.撤去外力后,求: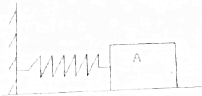 水平桌面上木块质量为15千克,与桌面之间的最大静摩擦力为为60牛.弹簧的劲度系数k=5000牛/米,如图所示,在木块A上施加向左的水平推力,当弹簧被外力压缩1厘米时,撤去外力后,物体将处于静止状态,此时木块受到的摩擦力为50牛,当压缩量大于1.2厘米时,撤去外力后,木块将不能保持静止状态.
水平桌面上木块质量为15千克,与桌面之间的最大静摩擦力为为60牛.弹簧的劲度系数k=5000牛/米,如图所示,在木块A上施加向左的水平推力,当弹簧被外力压缩1厘米时,撤去外力后,物体将处于静止状态,此时木块受到的摩擦力为50牛,当压缩量大于1.2厘米时,撤去外力后,木块将不能保持静止状态.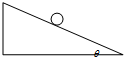 如图所示,在水平方向的匀强电场中,一个电量为-q,质量为m的带电小球静止在倾角为θ的光滑绝缘斜面上.求:
如图所示,在水平方向的匀强电场中,一个电量为-q,质量为m的带电小球静止在倾角为θ的光滑绝缘斜面上.求: 如图所示,有一内表面光滑的金属盒,底面长为L=1.2m,质量为m1=1kg,放在水平面上,与水平面间的动摩擦因数为μ=0.2,在盒内最右端放一半径为r=0.1m的光滑金属球,质量为m2=1kg,现在盒的左端,给盒一个初速度v=3m/s(盒壁厚度,球与盒发生碰撞的时间和能量损失均忽略不计,g取10m/s2)求:
如图所示,有一内表面光滑的金属盒,底面长为L=1.2m,质量为m1=1kg,放在水平面上,与水平面间的动摩擦因数为μ=0.2,在盒内最右端放一半径为r=0.1m的光滑金属球,质量为m2=1kg,现在盒的左端,给盒一个初速度v=3m/s(盒壁厚度,球与盒发生碰撞的时间和能量损失均忽略不计,g取10m/s2)求: